Fasor

Fasor
Para las siglas de Frequency Addition Source of Optical Radiation, véase FASOR.
Diagrama vectorial de la impedancia de distintos elementos de un circuito expresada de forma fasorial. El vector rojo es la impedancia total en serie, suma de los otros tres fasores.

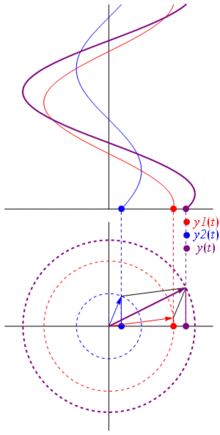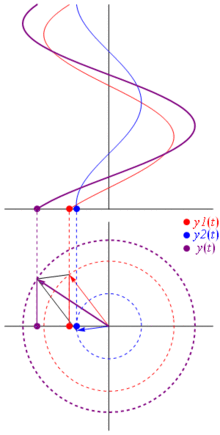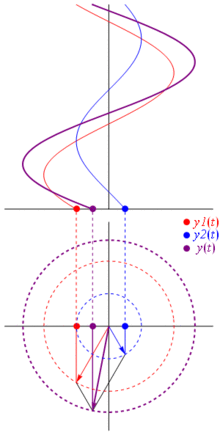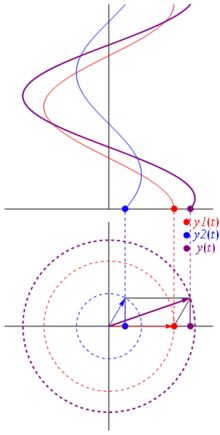
Un fasor es un vector utilizado para representar una onda, de forma que el vector suma de varios fasores puede ser utilizado para determinar la magnitud y fase de varias ondas después de procesos de interferencia. Los fasores se utilizan directamente en óptica, ingeniería de telecomunicaciones y acústica. La longitud del fasor da la amplitud y el ángulo entre el mismo y el eje-x la fase angular. Debido a las propiedades de la matemática de ondas, en electrónica los fasores se utilizan habitualmente en el análisis rudimentario de circuitos en AC. Finalmente, los fasores pueden ser utilizados para describir el movimiento de un oscilador. Las proyecciones del fasor en los ejes x e y tiene diferentes significados físicos.

Los fasores se usan comúnmente sobre todo para resolver visualmente problemas del tipo "existen varias ondas de frecuencia similar pero fases y amplitudes diferentes interfiriendo sobre un punto, ¿cual es la intensidad resultante?". Para solventar este problema, se dibuja un fasor para cada una de las ondas, y después simplemente se aplica la suma vectorial sobre ellos. La longitud del vector resultante en la amplitud de la onda resultante, y su longitud puede elevarse al cuadrado para obtener la intensidad. Nótese que mientras que la suma de varias ondas seno no es necesariamente otra onda seno, la suma de varias ondas sinusoidales de la misma frecuencia sí lo es, permitiendo leer la fase resultante como el ángulo del fasor resultante.

Contenido

Definición

Evolución de dos magnitudes senoidales de la misma frecuencia y de su suma en forma temporal y fasorial.

Una sinusoide u onda seno está definida como una función de la forma (la razón de utilizar una onda coseno en lugar de un seno será entendida posteriormente)

y = Acos(ωt + ϕ)

donde

  • y es la cantidad que varía con el tiempo
  • ϕ es una constante (en radianes) conocida como el ángulo de fase de la sinusoide
  • A es una constante conocida como la amplitud de la sinusoide. Es el valor de pico de la función.
  • ω es la frecuencia angular dada por ω = 2πf donde f es la frecuencia.
  • t es el tiempo.

Esto puede ser expresado como

y=\Re\{A\big(\cos{(\omega{}t+\phi)}+i\sin{(\omega t+\phi)}\big)\}\,\!

donde

  • i es la unidad imaginaria \sqrt{-1}. En ingeniería eléctrica se usa "j" en lugar de "i" para evitar las confusiones que se producirían con el mismo símbolo que se usa para designar la intensidad de la corriente eléctrica.
  • \Re(z)\,\! da la parte real del número complejo "z".

De forma equivalente, según la fórmula de Euler,

y=\Re(Ae^{i(\omega{}t+\phi)})\,\!
y=\Re(Ae^{i\phi}e^{i\omega{}t})\,\!

"Y", la representación fasor de esta sinusoide se define de la forma siguiente:

Y = Ae^{i \phi}\,

de forma que

y=\Re(Ye^{i\omega{}t})\,\!

Así, el fasor Y es el número complejo constante que contiene la magnitud y fase de la sinusoide. Para simplificar la notación, los fasores se escriben habitualmente en notación angular:

Y = A \angle \phi \,

Dentro de la Ingeniería Eléctrica, el ángulo fase se especifica habitualmente en grados sexagesimales en lugar de en radianes y la magnitud suele ser el valor eficaz en lugar del valor de pico de la sinusoide.

Leyes de circuitos

Utilizando fasores, las técnicas para resolver circuitos de corriente continua se pueden aplicar para resolver circuitos en corriente alterna. A continuación se indican las leyes básicas.

  • Ley de Ohm para resistencias: Una resistencia no produce retrasos en el tiempo, y por tanto no cambia la fase de una señal. Por tanto V=IR sigue siendo válida.
  • Ley de Ohm para resistencias, bobinas y condensadores: V=IZ donde Z es la impedancia compleja.
  • En un circuito AC se presenta una potencia activa (P) que es la representación de la potencia media en un circuito y potencia reactiva (Q) que indica el flujo de potencia atrás y adelante. Se puede definir también la potencia compleja S=P+jQ y la potencia aparente que es la magnitud de S. La ley de la potencia para un circuito AC expresada mediante fasores es entonces S=VI* (donde I* es el complejo conjugado de I).
  • Las Leyes de Kirchhoff son validas con fasores en forma compleja.

Dado esto, se pueden aplicar las técnicas de análisis de circuitos resistivos con fasores para analizar cicuitos AC de una sola frecuencia que contienen resistencias, bobinas y condensadores. Los circuitos AC con más de una frecuencia o con formas de onda diferentes pueden ser analizados para obtener tensiones y corrientes transformando todas las formas de onda en sus componentes sinusoidales y después analizando cada frecuencia por separado. Este método, resultado directo de la aplicación del principio de superposición, no se puede emplear para el cálculo de potencias, ya que éstas no se pueden descomponer linealmente al ser producto de tensiones e intensidades. Sin embargo, sí es válido resolver el circuito mediante métodos de superposición y, una vez obtenidos V e I totales, calcular con ellos la potencia.

Transformada fasorial

La transformada fasorial o representación fasorial permite cambiar de forma compleja a forma trigonométrica:

V_m e^{j \phi } = \mathcal{P} \{ V_m cos( \omega t + \phi ) \}

donde la notación \mathcal{P} \{X\} se lee como "transformada fasorial de X"

La transformada fasorial transfiere la función sinusoidal del dominio del tiempo al dominio de los números complejos o dominio de la frecuencia.

Transformada fasorial inversa

La transformada fasorial inversa \mathcal{P}^{-1} permite volver del dominio fasorial al dominio del tiempo.

Aritmética fasorial

Lo mismo que con otras cantidades complejas, el uso de la forma exponencial polar Aeiϕ simplifica las multiplicaciones y divisiones, mientras que la forma cartesiana (rectangular) a + ib simplifica las sumas y restas.

Véase también

Enlaces externos


Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • FASOR — Saltar a navegación, búsqueda Para el vector utilizado para representar una onda, véase fasor. En física del láser, FASOR es el acrónimo del inglés Frequency Addition Source of Optical Radiation (Fuente de Radiación Óptica por Suma de… …   Wikipedia Español

  • FASOR — can refer to: * FASOR (laser physics), Frequency Addition Source of Optical Radiation * Forward Air Spring Operated Return, a part of a paintball gun * Forward Area Sonar Research * Army Family Advocacy System of Records * Fasor , a Hungarian… …   Wikipedia

  • fäsör — s ( en, er) konstnär el. författare som är tekniskt skicklig men saknar originalitet och högre konstnärlig ambition …   Clue 9 Svensk Ordbok

  • Horno cuerpo negro — Este artículo está huérfano, pues pocos o ningún artículo enlazan aquí. Por favor, introduce enlaces hacia esta página desde otros artículos relacionados. La …   Wikipedia Español

  • Corriente alterna — Saltar a navegación, búsqueda Figura 1: Onda senoidal. Se denomina corriente alterna (abreviada CA en español y AC en inglés, de Alternating Current) a la corriente eléctrica en la que la magnitud y dirección varían cíclicamente. La forma de onda …   Wikipedia Español

  • Frequency Addition Source of Optical Radiation — In physics, a FASOR is an acronym for Frequency Addition Source of Optical Radiation. It is a device similar to a laser where the emitted light is produced in a sum frequency generation process from two laser sources that operate at a different… …   Wikipedia

  • Army Family Advocacy System of Records — The Army Family Advocacy System of Records (FASOR) is a program organized by the US Army Family Advocacy Program (FAP) to watch for and prevent mistreatment of the families of members of the US armed forces.External links*… …   Wikipedia

  • Zsigmond Quittner — (February 13 1859 – October 25 1918) was a Hungarian architect.CareerQuittner was born in Pest in 1859. He studied for his degree in Munich and worked in Budapest from 1880. His style is eclectic, a commercial version of the Vienna Secession. He… …   Wikipedia

  • Análisis de circuitos RLC de corriente alterna — Saltar a navegación, búsqueda El Análisis de circuitos RLC corriente alterna es una rama de la electrónica que detalla la resolución de las ecuaciones que definen estos circuitos, permitiendo así el análisis de su funcionamiento. A parte de… …   Wikipedia Español

  • Impedancia — La impedancia es una magnitud que establece la relación (cociente) entre la tensión y la intensidad de corriente. Tiene especial importancia si la corriente varía en el tiempo, en cuyo caso, ésta, la tensión y la propia impedancia se describen… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”