- Función inyectiva
-
En matemáticas, una función
 es inyectiva si a cada valor del conjunto
es inyectiva si a cada valor del conjunto  (dominio) le corresponde un valor distinto en el conjunto
(dominio) le corresponde un valor distinto en el conjunto  (imagen) de
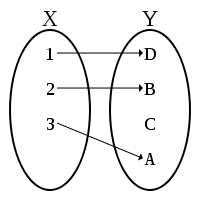
(imagen) de  . Es decir, a cada elemento del conjunto Y le corresponde un solo valor de X tal que, en el conjunto X no puede haber dos o más elementos que tengan la misma imagen.
. Es decir, a cada elemento del conjunto Y le corresponde un solo valor de X tal que, en el conjunto X no puede haber dos o más elementos que tengan la misma imagen.Así, por ejemplo, la función de números reales
 , dada por
, dada por  no es inyectiva, puesto que el valor 4 puede obtenerse como f(2) y f( − 2). Pero si el dominio se restringe a los números positivos, obteniendo así una nueva función
no es inyectiva, puesto que el valor 4 puede obtenerse como f(2) y f( − 2). Pero si el dominio se restringe a los números positivos, obteniendo así una nueva función  entonces sí se obtiene una función inyectiva.
entonces sí se obtiene una función inyectiva.Contenido
Definición formal
De manera más precisa, una función
 es inyectiva cuando se cumple alguna de las dos afirmaciones equivalentes:
es inyectiva cuando se cumple alguna de las dos afirmaciones equivalentes:- Si x1,x2 son elementos de
 tales que f(x1) = f(x2), necesariamente se cumple x1 = x2.
tales que f(x1) = f(x2), necesariamente se cumple x1 = x2. - Si x1,x2 son elementos diferentes de
 , necesariamente se cumple
, necesariamente se cumple 
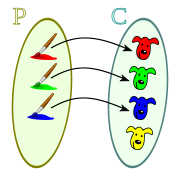
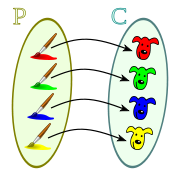
Los siguientes diagramas corresponden a función inyectiva:
Cardinalidad e inyectividad
Dados dos conjuntos
 y
y  , entre los cuales existe una función inyectiva
, entre los cuales existe una función inyectiva  tienen cardinales que cumplen:
tienen cardinales que cumplen:
Si además existe otra aplicación inyectiva
 , entonces puede probarse que existe una aplicación biyectiva entre A y B.
, entonces puede probarse que existe una aplicación biyectiva entre A y B.Ejemplos
- Para cualquier conjunto X y subconjunto S de X el mapa de la inclusión S → X (el cual envía cualquier elemento s de S para si mismo) es inyectiva. En particular, la función identidad X → X es siempre inyectiva (y de hecho biyectiva).
- La función f : R → R definida por f(x) = 2x + 1 es inyectiva.
- La función g : R → R definida por g(x) = x2 no es inyectiva, porque (por ejemplo) g(1) = 1 = g(−1). No obstante, si g se redefine de manera que su dominio es los números reales no negativos [0,+∞), entonces g es inyectiva.
- La función exponencial exp : R → R definida por exp(x) = ex es inyectiva (pero no sobreyectiva, porque no genera números negativos, los cuales no tienen relación con ningún valor de x).
- El logaritmo natural En la función ln : (0, ∞) → R definida por x ↦ ln x es inyectiva.
- La función g : R → R definida por g(x) = xn − x no es inyectiva, ya que, por ejemplo, g(0) = g(1).
En términos más generales, cuando X e Y están ambos en la recta real R, a continuación, una función inyectiva f : R → R es aquella cuya gráfica nunca es cruzada por una línea horizontal más de una vez. Este principio se conoce como la prueba de línea horizontal.
Véase también
Categoría:- Tipos de funciones
- Si x1,x2 son elementos de
Wikimedia foundation. 2010.