Función recíproca

Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas.
Puedes añadirlas así o avisar al autor principal del artículo en su página de discusión pegando: {{subst:Aviso referencias|Función recíproca}} ~~~~

Para otros usos de este término, véase Inverso multiplicativo.

Una función ƒ y su inversa o recíproca ƒ ^–1. Como ƒ aplica a en 3, la inversa ƒ ^–1 lleva 3 de vuelta en a.

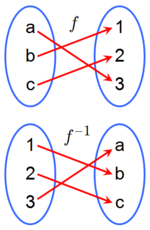
En matemáticas, si f es una aplicación o función que lleva elementos de I en elementos de J, en ciertas condiciones será posible definir la aplicación f ^-1 que realice el camino de vuelta de J a I. En ese caso diremos que f ^-1 es la aplicación inversa o recíproca de f.

Contenido

1 Definiciones formales
- 1.1 Definiciones alternativas
- 1.2 Notación alternativa
2 Propiedades algebraicas
3 Propiedades analíticas de funciones reales de una variable
4 Ejemplos
5 Véase también

Definiciones formales

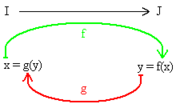
Sea f una función real inyectiva, cuyo dominio sea el conjunto I, es decir, creciente o decreciente en el conjunto I, y cuya imagen sea el conjunto J. Entonces, la función recíproca o inversa de f, denotada f ^-1, es la función de dominio J e imagen I definida por la siguiente regla:

$f(x) = y\Leftrightarrow{}f^{-1}(y) = x\text{.}\,\!$

Destaquemos que f ^-1, al igual que f, es una aplicación biyectiva, que queda determinada de modo único por f y que cumple:

$f^{-1} \circ f = id_i$ y
$f \circ f^{-1}=id_j$ .

De hecho, estas dos últimas propiedades caracterizan a la función inversa, como muestra la siguiente definición alternativa.

Definiciones alternativas

Dadas dos aplicaciones y las propiedades:

$g \circ f = id_I$ y
$f \circ g=id_J$ ,

entonces:

Si se cumple 1) entonces f es inyectiva y g sobreyectiva, y diremos que g es inversa por la izquierda de f.
Si se cumple 2) entonces g es inyectiva y f sobreyectiva, y diremos que g es inversa por la derecha de f.
Si se cumplen simultáneamente 1) y 2) entonces f y g son biyectivas y g es la inversa de f.

Este último punto se usa con frecuencia como definición de función inversa.

Notación alternativa

La notacion tradicional $f - 1$ puede ser confusa. Una notación alternativa utilizada en teoría de conjuntos es usar una estrella:

$f^\star:B \rightarrow A$ como alternativa a $f^{-1} \,$ .

Propiedades algebraicas

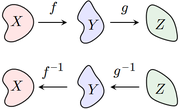
Inversión del orden en la composición de funciones.

La recíproca de la composición de dos funciones viene dada por la fórmula

$(g \circ f)^{-1} = f^{-1} \circ g^{-1}$

Obsérvese que se invierte el orden de f y g, pues para deshacer el camino avanzado primero por f y después por g, habrá que empezar deshaciendo este último por medio de g^–1 y terminar con f^–1,

La recíproca de la recíproca de una función es la propia función:

$\left(f^{-1}\right)^{-1} = f$

Esta propiedad se deduce de la simetría que hay en las fórmulas: $f^{-1} \circ f = Id_{X}$ y $f \circ f^{-1} = Id_{Y}$ .

Propiedades analíticas de funciones reales de una variable

Continuidad

f y g son simultáneamente continuas: Si una lo es, también lo será la otra. Sin embargo, es posible que ninguna lo sea: Por ejemplo se puede definir f así: si x es racional, f(x) = x, y si es irracional, f(x) = -x. En este caso muy particular g = f.

Además, en tal caso f y g son monótonas y tienen el mismo sentido de variación (ver la figura).

Gráfica de la función inversa

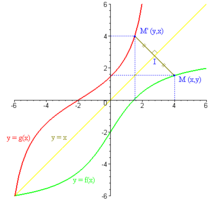
Ejemplo de una función f y de su recíproca g, donde los respectivos dominios de definición son I = [ -6; 6 ] y J = [ -6 ; 2.

Las gráficas que representan f y g son simétricas con relación a la primera diagonal, es decir, la recta Δ: y = x. En efecto, esta simetría envía un punto cualquiera M(x,y) sobre el punto M´(y,x). M pertenece a la curva de f si y sólo si M´ pertenece a la de g, porque la primera condición se escribe y = f(x) y la segunda x = g(y) y son por definición equivalentes.

Las tangentes en M y M´ tienen pendientes inversas. Es un efecto de la simetría anterior, y es la ilustración geométrica de la relación ya vista g'(y)· f '(x) = 1.

Derivabilidad

f y g son simultáneamente derivables: Si una lo es, también lo será la otra, con tal de aceptar valores infinitos de las derivadas de f y g.

Además, en tal caso, para cualquier x de I, si notamos y = f(x), entonces por regla de la cadena tenemos que g'(y)· f'(x) = 1. La derivada de g se obtiene así fácilmente a partir de la de f (vean los ejemplos al final).

Ejemplos

Por construcción misma, la función raíz cuadrada es la recíproca de la función "cuadrada" con dominio los reales no negativos, $x \rightarrow x^2$ Es decir, las dos funciones siguientes son una recíproca de la otra:

$\begin{cases} f:\R^+ \to \R^+ \\ x \mapsto x^2 \end{cases} \qquad \begin{cases} g:\R^+ \to \R^+ \\ x \mapsto \sqrt{x} \end{cases} \qquad f\circ g (x)= g\circ f (x) = x$

Más generalmente, la raíz positiva de orden n de un número positivo es la recíproca de $x \rightarrow x^n$ .
También por construcción, la exponencial es la recíproca del logaritmo.
Por definición misma, arccos, arcsen y arctan son las recíprocas de las funciones trigonométricas coseno, seno y tangente, lo que permite hallar sus derivadas:

Para

f (x) = cos(x) = y

g (y) = f - 1 (y) = arccos(y)

, y utilizando

cos 2 (x) + sin 2 (x) = 1

se obtiene: $g'(y) = \frac{1}{f'(x)} = \frac{1}{-\sin(x)} = \frac{1}{-\sqrt{1-\cos^2(x)}} = \frac{-1}{\sqrt{1-y^2}}$

Para

f (x) = tan(x) = y

g (y) = f - 1 (y) = arctan(y)

, y utilizando

tan '(x) = 1 + tan 2 (x)

se obtiene: $g'(y) = \frac{1}{f'(x)} = \frac{1}{1 + \tan^2(x)} = \frac{1}{1+y^2}$

Se generaliza el concepto de función recíproca a otros conjuntos de números, en particular a los complejos, donde el logaritmo (con un dominio restringido) y la exponencial siguen siendo funciones recíprocas.

En otras ocasiones una función inversa puede existir y estar bien definida pero no pude escribirse en términos de funciones elementales, como sucede con la función f:

$\begin{cases} f:\R \to [-1,1]\\ x \mapsto \cfrac{1}{2\pi}\left[ \ln\left(\cfrac{x^2+x\sqrt{2}+1}{x^2-x\sqrt{2}+1}\right) + 2\arctan(x\sqrt{2}+1)+2\arctan(x\sqrt{2}-1) \right] = \sum_{k=0}^\infty \cfrac{(-1)^k x^k}{4k+1}\end{cases}$

Aunque la función recíproca se puedde aproximar como serie de Taylor:

$f^{-1}(x) \approx x + \frac{x^5}{5} + \dots$

Véase también

Teorema de la función inversa, condiciones suficientes para la existencia de una función inversa continua y diferenciable.

Categoría:

Funciones

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

Función recíproca — Definición Sea f una función real biyectiva, cuyo dominio (conjunto de definición) es I y cuyo conjunto imagen es J = f(I). Por ser biyectiva, f admite una función recíproca o inversa, denotada f 1. Definición: g es la función recíproca de f si… … Enciclopedia Universal
función — (Del lat. functĭo, ōnis). 1. f. Capacidad de actuar propia de los seres vivos y de sus órganos, y de las máquinas o instrumentos. 2. Tarea que corresponde realizar a una institución o entidad, o a sus órganos o personas. 3. Acto solemne,… … Diccionario de la lengua española
Función — (Del lat. functio, onis.) ► sustantivo femenino 1 BIOLOGÍA Actividad o capacidad de acción específica de un ser vivo y de sus órganos: ■ la función del riñón; la función clorofílica. 2 Desempeño de un cargo u oficio: ■ el vicepresidente desempeña … Enciclopedia Universal
Función matemática — En la imagen se muestra una función entre un conjunto de polígonos y un conjunto de números. A cada polígono le corresponde su número de lados. En matemáticas, se dice que una magnitud o cantidad es función de otra si el valor de la primera… … Wikipedia Español
Función raíz — Sea n un número natural no nulo. La función x → xn define una biyección, de R hacia R si n es impar, y de si es par. Se llama enésima raíz, o raíz de orden n su función recíproca, y se nota: . (dos notaciones posibles) Para todo n natural, a … Enciclopedia Universal
Función trascendente — Una función trascendente es una función que no satisface una ecuación polinomial cuyos coeficientes sean a su vez polinomios; esto contrasta con las funciones algebraicas, las cuales satisfacen dicha ecuación.[1] En otras palabras, una función… … Wikipedia Español
Función gamma — en el eje real. Valor absoluto de la función gamma en el plano complejo … Wikipedia Español
Función raíz — Se ha sugerido que Raíz enésima de un número sea fusionado en este artículo o sección (discusión). Una vez que hayas realizado la fusión de artículos, pide la fusión de historiales aquí. Se llama enésima raíz, o raíz de orden n su función… … Wikipedia Español
Función zeta de Ihara — La función zeta de Ihara tiene similaridades con la función zeta de Selberg, y es utilizada para relacionar el espectro de la matriz de adyacencia de un gráfico G a su característica de Euler. Definición La función zeta de Ihara fue inicialmente… … Wikipedia Español
Función exponencial — La función exponencial es la recíproca de la función logaritmo natural. Con esa definición, su dominio es R, pero se puede ampliar al cuerpo de los complejos. Esta función se nota exp: R → R+* donde e es la base de los logaritmos naturales. * * * … Enciclopedia Universal

Los diccionarios y las enciclopedias sobre el Académico

Función recíproca

Contenido