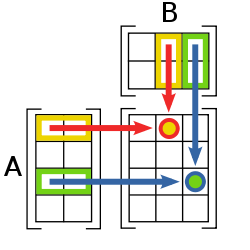
Multiplicación de matrices

En matemática, la multiplicación o producto de matrices es la operación de multiplicación que se efectúa entre dos matrices, o bien entre una matriz y un escalar.

Al igual que la multiplicación aritmética, su definición es instrumental, es decir, viene dada por un algoritmo capaz de resolverla. El algoritmo que resuelve la multiplicación matricial es diferente del que resuelve la multiplicación de dos números. La diferencia principal es que la multiplicación de matrices no cumple con la propiedad de conmutatividad.

Contenido

1 Multiplicación de una matriz por un escalar
- 1.1 Propiedades
2 Multiplicación de una matriz por otra matriz
- 2.1 Propiedades
3 Aplicaciones
- 3.1 Sistemas de ecuaciones
4 Referencias
5 Enlaces externos

Multiplicación de una matriz por un escalar

Dada una matriz A de m filas y n columnas, lo que podemos denotar como:

$A:=(a_{ij})_{m \times n}$

la multiplicación de A por un escalar k, que se denota k·A, k×A o simplemente kA, está definida como:

$kA:=(k\cdot a_{ij})_{m \times n}$

es decir, corresponde a la matriz conformada por cada elemento de la matriz multiplicado por dicho escalar.

Gráficamente, si

$A = \begin{bmatrix} a_{11} & ... & a_{1n} \\ ... & ... & ... \\ a_{m1} & ... & a_{mn} \end{bmatrix}$

$k\in\mathbb{R},$

entonces

$kA = \begin{bmatrix} ka_{11} & ... & ka_{1n} \\ ... & ... & ... \\ ka_{m1} & ... & ka_{mn} \end{bmatrix}$

La multiplicación por escalar es análoga a la suma o resta de matrices, y cumple con las mismas características de la multiplicación aritmética. En efecto, podemos llegar al mismo resultado sumando k veces la misma matriz A entre sí.

Propiedades

Sean A, B matrices y c, d escalares, la multiplicación de matrices por escalares cumple con las siguientes propiedades:

Propiedad	Descripción
Clausura	cA es también una matriz
Elemento neutro	Existe el elemento neutro uno, de manera que 1·A = A
Propiedad asociativa	(cd)A = c(dA)
Propiedad distributiva - De escalar - De matriz	c(A+B) = cA+cB (c+d)A = cA+dA

Multiplicación de una matriz por otra matriz

Los resultados en las posiciones marcadas dependen de las filas y columnas de sus respectivos colores.

Dadas dos matrices A y B, tales que el número de columnas de la matriz A es igual al número de filas de la matriz B; es decir:

$A:=(a_{ij})_{m \times n}$ y $B:=(b_{ij})_{n \times p}$

la multiplicación de A por B, que se denota A·B, A×B o simplemente AB, está definida como:

$AB:=(c_{ij})_{m \times p}$

donde cada elemento c_i,j está definido por:

$c_{ij} = \sum_{r=1}^n a_{ir}b_{rj}$

Gráficamente, si

$A = \begin{bmatrix} a_{11} & ... & a_{1n} \\ ... & ... & ... \\ a_{m1} & ... & a_{mn} \end{bmatrix}$

$B = \begin{bmatrix} b_{11} & ... & b_{1p} \\ ... & ... & ... \\ b_{n1} & ... & b_{np} \end{bmatrix}$

entonces

$AB = \begin{bmatrix} a_{11}b_{11}+...+a_{1n}b_{n1} & ... & a_{11}b_{1p}+...+a_{1n}b_{np} \\ ... & ... & ... \\ a_{m1}b_{11}+...+a_{mn}b_{n1} & ... & a_{m1}b_{1p}+...+a_{mn}b_{np} \end{bmatrix}$

Propiedades

Sean A, B y C matrices para las cuales la multiplicación entre ellas está bien definida, es decir, tales que sus elementos pertenecen a un grupo donde la multiplicación está definida, y de manera que el número de filas y de columnas permite realizar la multiplicación; entonces se cumplen las siguientes propiedades:

Propiedad	Descripción
Clausura	AB es también una matriz
Elemento neutro	Si A es una matriz cuadrada de tamaño m, entonces la matriz identidad I_m×m es elemento neutro, de manera que I·A = A·I = A
Propiedad asociativa	(AB)C = A(BC)
Propiedad distributiva - Por la derecha - Por la izquierda	(A + B)C = AC + BC C(A + B) = CA + CB

El producto de dos matrices generalmente no es conmutativo, es decir, AB ≠ BA. La división entre matrices, es decir, la operación que podría producir el cociente A / B, no se encuentra definida. Sin embargo, existe el concepto de matriz inversa, sólo aplicable a las matrices invertibles.

Finalmente, note que tanto la multiplicación de una matriz por un escalar, como la multiplicación de dos escalares, puede representarse mediante una multiplicación de dos matrices.

Demostración de la propiedad asociativa

Sean A una matriz de mxn; B una matriz de nxp; y C un matriz de pxq. Entonces, AB sera una matriz de mxp. Del mismo modo, BC sera una matriz de nxq. Por lo tanto, usando sumatoria, verificaremos la propiedad asociativa del producto de matrices, es decir, (AB)C=A(BC). Para AB:

$AB=\sum_{k=1}^n a_{ik}b_{kj}=D=(d_{ij})$

Luego, multiplicando D por C:

$DC=\sum_{l=1}^p d_{il}c_{lj}$

Reemplazando D por AB:

(1) $(AB)C=\sum_{l=1}^p(\sum_{k=1}^n a_{ik}b_{kl})c_{lj}=\sum_{l=1}^p \sum_{k=1}^n a_{ik}b_{kl}c_{lj}$

Ahora, para BC:

$BC=\sum_{l=1}^p b_{il}c_{lj}=E=(e_{ij})$

Luego, multiplicando A por E:

$AE=\sum_{k=1}^n a_{ik}e_{kj}$

Reemplazando E por BC:

(2) $A(BC)=\sum_{k=1}^n a_{ik}(\sum_{l=1}^n b_{kl}c_{lj})=\sum_{k=1}^n \sum_{l=1}^p a_{ik}b_{kl}c_{lj}$

Con lo que verificamos que (1) y (2) son iguales y se cumple la propiedad asociativa:

$(AB)C=A(BC)\,$

Aplicaciones

La multiplicación de matrices es muy útil para la resolución de sistemas de ecuaciones de muchas variables, dado que son muy cómodas para ser implementadas mediante un computador. El cálculo numérico se basa en gran parte de estas operaciones, al igual que poderosas aplicaciones tales como MATLAB. También actualmente se utiliza mucho en el cálculo de microarrays, en el área de bioinformática.

Sistemas de ecuaciones

Consideremos el caso más sencillo, el de las matrices cuadradas de orden 2, es decir cuando n = m = 2. Las aplicaciones lineales del plano real que, al punto M(x₁,x₂) hacen corresponder el punto N(y₁,y₂) se expresan como un sistema de dos ecuaciones con dos variables. Las matrices permiten escribirlos más rápidamente. Así, por ejemplo, el sistema:

$\left \{ \begin{matrix} y_1 = a x_1 + b x_2\\ y_2 = c x_1 + d x_2 \end{matrix} \right.$

se escribe de forma matricial así:

$\begin{pmatrix} y_1\\ y_2 \end{pmatrix} = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x_1\\ x_2 \end{pmatrix}$

Como se ve, en la notación matricial, las variables soló aparecen una vez, así como el símbolo "=", y los signos "+" ni se escriben. Los ahorros de tiempo y energía no son enormes aquí, pero crecen con las dimensiones de la matriz.

Ahora bien, las aplicaciones lineales se pueden sumar, lo que daría la adición de las matrices que se definió arriba, pero no se pueden multiplicar. Sin embargo, existe otra operación, universal en el campo de las aplicaciones: la composición, es decir aplicar sucesivamente dos o más funciones a un objeto. Al componer:

$\left \{ \begin{matrix} z_1 = e y_1 + f y_2\\ z_2 = g y_1 + h y_2 \end{matrix} \right. \mbox{ con } \left \{ \begin{matrix} y_1 = a x_1 + b x_2\\ y_2 = c x_1 + d x_2 \end{matrix} \right.$

obtenemos:

$\left \{ \begin{matrix} z_1 = e(a x_1 + b x_2) + f(c x_1 + d x_2) = (ea + fc)x_1 + (eb + fd)x_2\\ z_2 = g(a x_1 + b x_2) + h(c x_1 + d x_2) = (ga + hc)x_1 + (gb + hd)x_2 \end{matrix} \right.$

lo que corresponde a la matriz:

$\begin{pmatrix} ea + fc & eb + fd\\ ga + hc & gb + hd \end{pmatrix}$

Por lo tanto se define el producto de matrices así:

$\begin{pmatrix} e & f \\ g & h \end{pmatrix}\begin{pmatrix} a & b \\ c & d \end{pmatrix} = \begin{pmatrix} ea + fc & eb + fd\\ ga + hc & gb + hd \end{pmatrix}$

Referencias

El contenido de este artículo incorpora material de una entrada de la Enciclopedia Libre Universal, publicada en español bajo la licencia Creative Commons Compartir-Igual 3.0.

Enlaces externos

Wikilibros

Wikilibros alberga un libro o manual sobre Optimización del Producto de Matrices.
Calculadora de matrices (Multiplicación)

Categoría:

Matrices

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

Multiplicación — Para saber cómo multiplicar, véase Algoritmo de multiplicación. Propiedad conmutativa: 3×4 = 12 = 4×3 doce elementos pueden ser ordenados en tres filas de cuatro, o cuatro columnas de tres. La multiplicación es una operación matemática que… … Wikipedia Español
Grupo de Lie — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar … Wikipedia Español
Algoritmo de Strassen — En la disciplina matemática del álgebra lineal, el algoritmo de Strassen, llamado así por Volker Strassen, es un algoritmo usado para la multiplicación de matrices. Es asintóticamente más rápido que el algoritmo de multiplicación de matrices… … Wikipedia Español
Cuaternión — Saltar a navegación, búsqueda Los cuaterniones son una extensión de los números reales, similar a la de los números complejos. Mientras que los números complejos son una extensión de los reales por la adición de la unidad imaginaria i, tal que i2 … Wikipedia Español
Matriz (matemática) — Se ha sugerido que Teoría de Matrices sea fusionado en este artículo o sección (discusión). Una vez que hayas realizado la fusión de artículos, pide la fusión de historiales aquí. Para otros usos de este término, véase Matriz. En matemáticas, una … Wikipedia Español
Volker Strassen — dando la conferencia del premio Knuth en SODA 2009. Volker Strassen es un matemático alemán, profesor emérito del departamento de matemáticas y estadística de la Universidad de Constanza.[1] … Wikipedia Español
Transformada rápida de Fourier — Para otros usos de este término, véase Transformación (desambiguación). FFT es la abreviatura usual (del inglés Fast Fourier Transform) de un eficiente algoritmo que permite calcular la transformada de Fourier discreta (DFT) y su inversa. La FFT… … Wikipedia Español
Grupo lineal general — En matemáticas, el grupo lineal general (GL) de un espacio vectorial , denotdo como , es el grupo formado por todos los isomorfismos de ese espacio. Cuando el espacio vectorial es siendo un cuerpo F (tal como o … Wikipedia Español
Mecánica matricial — La Mecánica matricial es una formulación de la mecánica cuántica creada por Werner Heisenberg, Max Born y Pascual Jordan en 1925. La mecánica matricial fue la primera definición completa y correcta de la mecánica cuántica. Extiende el modelo de… … Wikipedia Español
Álgebra de Lie — En matemática, un álgebra de Lie es la estructura algebraica que describe un conjunto de transformaciones infinitesimales. Su uso principal reside en el estudio de objetos geométricos tales como grupos de Lie y variedades diferenciables. El… … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Multiplicación de matrices

Contenido

Multiplicación de una matriz por un escalar

Propiedades

Multiplicación de una matriz por otra matriz

Propiedades

Aplicaciones

Sistemas de ecuaciones

Referencias

Enlaces externos

Mira otros diccionarios:

Compartir el artículo y extractos

Los diccionarios y las enciclopedias sobre el Académico

Wikipedia Español

Multiplicación de matrices

Contenido

Multiplicación de una matriz por un escalar

Propiedades

Multiplicación de una matriz por otra matriz

Propiedades

Aplicaciones

Sistemas de ecuaciones

Referencias

Enlaces externos

Mira otros diccionarios:

Compartir el artículo y extractos

Link directo