Resonancia magnética nuclear

Resonancia magnética nuclear
Imagen del cerebro humano obtenida por resonancia magnética.
Imágenes de un corazón humano bombeando.

La resonancia magnética nuclear (RMN) es un fenómeno físico basado en las propiedades mecánico-cuánticas de los núcleos atómicos. RMN también se refiere a la familia de métodos científicos que explotan este fenómeno para estudiar moléculas (espectroscopia de RMN), macromoléculas (RMN biomolecular), así como tejidos y organismos completos (imagen por resonancia magnética).

Todos los núcleos que poseen un número impar de protones o neutrones tienen un momento magnético y un momento angular intrínseco, en otras palabras, tienen un espín > 0. Los núcleos más comúnmente empleados en RMN son el protón (1H, el isótopo más sensible en RMN después del inestable tritio, 3H), el 13C y el 15N, aunque los isótopos de núcleos de muchos otros elementos (2H, 10B, 11B, 14N, 17O, 19F, 23Na, 29Si, 31P, 35Cl, 113Cd, 195Pt) son también utilizados.

Las frecuencias a las cuales resuena un átomo (i. e. dentro de una molécula) son directamente proporcionales a la fuerza del campo magnético ejercido, de acuerdo con la ecuación de la frecuencia de precesión de Larmor. La literatura científica hasta el 2008 incluye espectros en un gran intervalo de campos magnéticos, desde 100 nT hasta 20 T). Los campos magnéticos mayores son a menudo preferidos puesto que correlacionan con un incremento en la sensibilidad de la señal. Existen muchos otros métodos para incrementar la señal observada. El incremento del campo magnético también se traduce en una mayor resolución espectral, cuyos detalles son descritos por el desplazamiento químico y el efecto Zeeman.

La RMN estudia los núcleos atómicos al alinearlos a un campo magnético constante para posteriormente perturbar este alineamiento con el uso de un campo magnético alterno, de orientación ortogonal. La resultante de esta perturbación es el fenómeno que explotan las distintas técnicas de RMN. El fenómeno de la RMN también se utiliza en la RMN de campo bajo, la RMN de campo terrestre y algunos tipos de magnetómetros.

Contenido

Aplicaciones más comunes

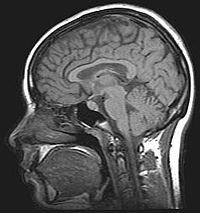
La resonancia magnética hace uso de las propiedades de resonancia aplicando radiofrecuencias a los átomos o dipolos entre los campos alineados de la muestra, y permite estudiar la información estructural o química de una muestra. La RM se utiliza también en el campo de la investigación de ordenadores cuánticos. Sus aplicaciones más frecuentes se encuentran ligadas al campo de la medicina, la bioquímica y la química orgánica. Es común denominar "resonancia magnética" al aparato que obtiene imágenes por resonancia magnética (MRI, por las siglas en inglés de "Magnetic Resonance Imaging").

Historia

Descubrimiento

Raymond Damadian Vahan, un americano-armenio médico e inventor de la primera RM (resonancia magnética) de la máquina de exploración - una de las herramientas de diagnóstico más útiles de nuestro tiempo. [1] Su investigación en sodio y potasio en las células vivas lo llevó a sus primeros experimentos con resonancia magnética nuclear (RMN), que le llevó a proponer el primer escáner de cuerpo MR en 1969. Damadian descubrió que los tumores y el tejido normal se pueden distinguir en vivo por resonancia magnética nuclear (RMN) a causa de sus tiempos de relajación. Damadian fue el primero en realizar una exploración completa del cuerpo de un ser humano en 1977 para diagnosticar el cáncer. Damadian inventó un aparato y método para el uso de RMN con seguridad y precisión para explorar el cuerpo humano, un método ahora conocido como la resonancia magnética (MRI)[2].

La resonancia magnética nuclear fue descrita y medida en rayos moleculares por Isidor Rabi en 1938.[1] Ocho años después, en 1946, Félix Bloch y Edward Mills Purcell refinan la técnica usada en líquidos y en sólidos, por lo que compartieron el Premio Nobel de física en 1952.[2]

Purcell había trabajado en el desarrollo del radar y sus aplicaciones durante la segunda guerra mundial en el Lab de Radiación del Instituto Tecnológico de Massachusetts. Su obra durante tal proyecto fue producir y detectar energía de radiofrecuencias, y sobre absorciones de tales energías de RF por la materia, precediendo a su codescubrimiento de la RMN.

Ellos se dieron cuenta de que los núcleos magnéticos, como 1H (protio) y 31P, podían absorber energía de RF cuando eran colocados en un campo magnético de una potencia específica y así lograban identificar los núcleos. Cuando esa absorción ocurre, los núcleos se describen como estando en resonancia. Diferentes núcleos atómicos dentro de una molécula resuenan a diferentes frecuencias de radio para la misma fuerza de campo magnética. La observación de tales frecuencias resonantes magnéticas de los núcleos presentes en una molécula permite al usuario entrenado descubrir información esencial, química y estructural acerca de las moléculas.

El desarrollo de la resonancia magnética nuclear como técnica de química analítica y de bioquímica fue paralela con el desarrollo de la tecnología electromagnética y su introducción al uso civil.

Principio físico

Espín nuclear

Las partículas elementales que componen al núcleo atómico (neutrones y protones), tienen la propiedad mecánico-cuántica intrínseca del espín. El espín de un núcleo está determinado por el número cuántico del espín I. Si el número combinado de protones y neutrones en un isótopo dado es par, entonces I = 0, i. e. no existe un espín general; así como los electrones se aparean en orbitales atómicos, de igual manera se asocian neutrones y protones en números pares (que también son partículas de espín ½ y por lo tanto son fermiones) para dar un espín general = 0.

Un espín distinto a cero, I, está asociado a un momento magnético distinto a cero, μ:

\ \mu = \gamma I

en donde γ es la proporción giromagnética. Esta constante indica la intensidad de la señal de cada isótopo usado en RMN.

Valores del momento angular del espín

El momento angular asociado al espín nuclear esta cuantizado. Esto significa que tanto la magnitud como la orientación del momento angular están cuantizadas (i.e. I solo puede tomar valores en un intervalo restringido). El número cuántico asociado se conoce como número cuántico magnético, m, y puede tomar valores enteros desde +I hasta -I. Por lo tanto, para cualquier núcleo, existe un total de 2I+1 estados de momento angular.


El componente z del vector de momento angular, Iz, es por lo tanto:

I_z = m \hbar

en la que \hbar es la constante de Planck reducida.

El componente z del momento magnético es simplemente:

\mu_z = \gamma I_z = m\gamma \hbar

Comportamiento del espín en un campo magnético

Consideremos un núcleo que posee un espín de ½, como 1H, 13C o 19F. Este núcleo tiene dos estados posibles de espín: m = ½ o m = -½ (que también se les llama 'arriba' y 'abajo', o α y β, respectivamente). Las energías de estos dos estados son degeneradas —lo cual significa que son las mismas. Por lo tanto las poblaciones de estos dos estados (i.e. el número de átomos en los dos estados) serán aproximadamente iguales en condiciones de equilibrio térmico.

Sin embargo, al poner este núcleo bajo un campo magnético, la interacción entre el momento magnético nuclear y el campo magnético externo promoverá que los dos estados de espín dejen de tener la misma energía. La energía del momento magnético μ bajo la influencia del campo magnético B0 (el subíndice cero se utiliza para distinguir este campo magnético de cualquier otro campo magnético utilizado) está dado por el producto escalar negativo de los vectores:

E = -{\mathbf B_0}\cdot{\mathbf \mu}= - \mu_z B_0

En el que el campo magnético ha sido orientado a lo largo del eje z.

Por lo tanto:

E = - m\hbar\gamma B_0

Como resultado, los distintos estados nucleares del espín tienen diferentes energías en un campo magnético ≠ 0. En otras palabras, podemos decir que los dos estados del espín de un espín ½ han sido alineados ya sea a favor o en contra del campo magnético. Si γ es positiva (lo cual es cierto para la mayoría de los isótopos) entonces m = ½ está en el estado de baja energía.

La diferencia de energía entre los dos estados es:

\Delta E = \hbar\gamma B_0

y esta diferencia se traduce en una pequeña mayoría de espines en el estado de baja energía.

La absorción de resonancia ocurre cuando esta diferencia de energía es excitada por radiación electromagnética de la misma frecuencia. La energía de un fotón es E = hν, donde ν es su frecuencia. Por lo tanto la absorción ocurrirá cuando:

\nu = \frac{\Delta E}{h}= \frac{\gamma B_0}{2\pi}

Estas frecuencias corresponden típicamente al intervalo de radiofrecuencias del espectro electromagnético. Esta es la absorción de resonancia que se detecta en RMN.

Apantallamiento nuclear

Podría parecer por lo dicho arriba que todos los núcleos del mismo núclido (y por lo tanto la misma γ) resuenan a la misma frecuencia. Este no es el caso. La perturbación más importante en las frecuencias de RMN para aplicaciones en RMN es el efecto de 'apantallamiento' que ejercen los electrones circundantes. En general, este apantallamiento electrónico reduce el campo magnético del núcleo (lo cual determina la frecuencia de la RMN). Como resultado, la brecha energética se reduce y la frecuencia requerida para alcanzar resonancia también se reduce. Este desplazamiento de la frecuencia de RMN dado por el ambiente químico se conoce como desplazamiento químico, y explica porque el RMN es una sonda directa de la estructura química. Si un núcleo está más apantallado, estará desplazado hacia 'campo alto' (menor desplazamiento químico) y si está más desapantallado, entonces estará desplazado hacia 'campo bajo' (mayor desplazamiento químico).[3]

A menos que la simetría local sea particularmente alta, el efecto de apantallamiento depende de la orientación de la molécula con respecto al campo externo. En RMN de estado sólido, el 'giro al ángulo mágico' (magic angle spinning) es necesario para disipar esta dependencia orientacional. Esto no se requiere en RMN convencional puesto que el movimiento rápido y desordenado de moléculas en solución disipa el componente anisótropo del corrimiento químico.

Digitalización mediante transformada de Fourier

Con la desalineación de los espines, es decir, la recuperación natural de la dirección y sentido de éstos una vez sometidos a la radiación electromagnética, generará unas emisiones a consecuencia de la liberación energética, los cuales serán captados por la antena receptora del escáner. Estas emisiones han de ir en concordancia con la Dim-Fase, siendo la compilación de todas estas emisiones el principio de la resonancia magnética.

Una vez finalizada toda la extracción de datos se procederá al trato de las mismas en el dominio de la frecuencia mediante el empleo de la transformada de Fourier, la cual nos facilitará la reconstrucción de la imagen final por pantalla. La frecuencia de la variación de una señal en el espacio se denomina "K", es decir, los datos compilados en el dominio de las frecuencias espaciales se denomina espacio K.

La finalidad de la creación de este espacio es poder aplicar las leyes matemáticas de Fourier, lo que permite identificar el lugar de procedencia de las emisiones en un determinado momento y, por lo tanto, su lugar de procedencia.

Espectroscopia de RMN

Artículo principal: Espectroscopia de resonancia magnética nuclear

La espectroscopia de RMN es una de las principales técnicas empleadas para obtener información física, química, electrónica y estructural sobre moléculas. Es una poderosa serie de metodologías que proveen información sobre la topología, dinámica y estructura tridimensional de moléculas en solución y en estado sólido. Asimismo, en los años 1998-2001 la resonancia magnética nuclear fue una de las técnicas más utilizadas para implementar algunos principios de las computadoras cuánticas.[4]

Bibliografía complementaria

  • Blümich, Bernhard, "RMN portátil", Investigación y Ciencia, 390, marzo de 2009, pp. 82-87.

Véase también

Referencias

  1. ↑ I.I. Rabi, J.R. Zacharias, S. Millman, P. Kusch (1938). «A New Method of Measuring Nuclear Magnetic Moment». Physical Review 53:  p. 318. doi:10.1103/PhysRev.53.318. 
  2. ↑ Filler, Aaron (2009). «The History, Development and Impact of Computed Imaging in Neurological Diagnosis and Neurosurgery: CT, MRI, and DTI». Nature Precedings. doi:10.1038/npre.2009.3267.5. 
  3. ↑ Introducción a la espectroscopía de RMN
  4. ↑ Hay una revisión de los logros de esos años, las dificultades fundamentales y algunas alternativas en: Jones, J.A. (2001). «Quantum computing and nuclear magnetic resonance» (en inglés). PhysChemComm 11. doi:10.1039/b103231n. pp.1-8. 
  1. Hornak, Joseph P. The Basics of NMR
  2. A. Carrington, A.D. McLachlan (1967). Introduction To Magnetic Resonance. Londres: Chapman and Hall. ISBN. 
  • G.E Martin, A.S. Zekter (1988). Two-Dimensional NMR Methods for Establishing Molecular Connectivity. N.York: VCH Publishers. p. 59. 
  • J.W. Akitt, B.E. Mann (2000). NMR and Chemistry. Cheltenham, RU: Stanley Thornes. pp. 273, 287. 
  • J.P. Hornak. «The Basics of NMR». Consultado el 23 de febrero de 2009.
  • J. Keeler (2005). Understanding NMR Spectroscopy. John Wiley & Sons. ISBN 0470017864. 
  • K. Wuthrich (1986). NMR of Proteins and Nucleic Acids. New York (NY), EEUU: Wiley-Interscience. 
  • J.M Tyszka, S.E Fraser, R.E Jacobs (2005). «Magnetic resonance microscopy: recent advances and applications». Current Opinion in Biotechnology 16 (1):  pp. 93–99. doi:10.1016/j.copbio.2004.11.004. 
  • L.O. Zufiría, J.F. Martínez (2006). «Aprendiendo los fundamentos de la resonancia magnética». Monografía SERAM 1 (1):  pp. 20. 
  • J.C. Edwards. «Principles of NMR». Process NMR Associates. Consultado el 23 de febrero de 2009.

Enlaces externos

Tutorial

Animaciones y simulaciones

Software

  • CARA - Computer Aided Resonance Assignment, libre, desarrollado por el grupo del Prof. Kurt Wüthrich
  • CCPN NMR software suite from community led Collaborative Computing Project for NMR.
  • Janocchio Conformation-dependent coupling and NOE prediction for small molecules.
  • Soft para procesar RMN del ACD/Labs para 1D y 2D espectros RMN. Interface DB diponible.
  • Soft predictivo RMN ACD/NMR Predictors
  • Soft de simulación RMN QSim
  • Soft libre para simular un espín acoplado a multiplets y a espectros DNMR WINDNMR-Pro
  • Soft para procesar RMN NMRPipe
  • RMN - Un programa de procesador de datos RMN para Macintosh.

Video

Wiki

  • NMR Wiki Proyecto abierto NMR, EPR, MRI web


Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • resonancia magnética nuclear — f. mét. explor. Método de reconstitución de imágenes anatómicas basado en las propiedades del momento magnético de los núcleos atómicos y que se consigue mediante la aplicación de un campo magnético. Permite determinar la estructura de los… …   Diccionario médico

  • Resonancia magnética nuclear — La resonancia magnética nuclear (RMN o NMR de sus siglas en inglés) es un fenómeno físico basado en las propiedades magnéticas que poseen los núcleos atómicos. La RMN permite alinear los campos magnéticos de diferentes átomos en la dirección de… …   Enciclopedia Universal

  • resonancia magnética nuclear (RMN) — Absorción selectiva de ondas de radio de muy alta frecuencia por ciertos núcleos atómicos sometidos a un campo magnético estacionario intenso. Núcleos que tienen por lo menos un protón o neutrón no apareado, actúan como pequeños imanes. Cuando… …   Enciclopedia Universal

  • Espectroscopia de resonancia magnética nuclear — Saltar a navegación, búsqueda La espectroscopia de resonancia magnética nuclear (RMN) es una técnica empleada principalmente en la elucidación de estructuras moleculares, aunque también se puede emplear con fines cuantitativos. Algunos núcleos… …   Wikipedia Español

  • Espectroscopia mediante resonancia magnética nuclear de proteínas — Saltar a navegación, búsqueda Introducción de la muestra en el espectrómetro RMN de alto campo magnético (800 MHz) del Pacific Northwest National Laboratory. La espectroscopía mediante resonancia magn …   Wikipedia Español

  • Espectroscopia de resonancia magnética nuclear — La espectroscopia de resonancia magnética nuclear es una técnica empleada principalmente en la elucidación de estructuras moleculares, aunque también se puede emplear con fines cuantitativos. Esta técnica se basa en el fenómeno físico de… …   Enciclopedia Universal

  • Resonancia magnética — Saltar a navegación, búsqueda Resonancia magnética (abreviado «RM») puede significar: Resonancia magnética nuclear Resonancia de espín electrónico Imagen por resonancia magnética (IRM) Imagen por resonancia magnética funcional (IRMf) Obtenido de… …   Wikipedia Español

  • resonancia magnética — ► locución FÍSICA NUCLEAR, MEDICINA Método de exploración electrorradiológico que se basa en la propiedad de ciertos núcleos atómicos de comportarse como pequeños imanes y que permite reconstruir imágenes anatómicas. * * * Absorción o emisión de… …   Enciclopedia Universal

  • Imagen por resonancia magnética — Imagen combinada IRM / PET de una cabeza Imágenes de una …   Wikipedia Español

  • imagen de resonancia magnética — (IRM) Imágenes médicas que utilizan la resonancia magnética nuclear como fuente de energía. Diccionario Mosby Medicina, Enfermería y Ciencias de la Salud, Ediciones Hancourt, S.A. 1999 …   Diccionario médico

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”