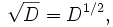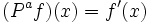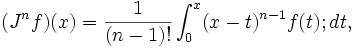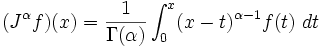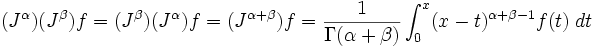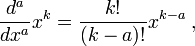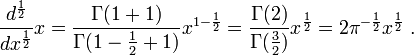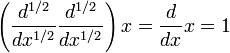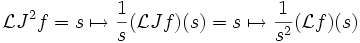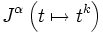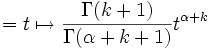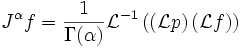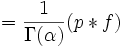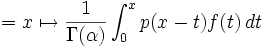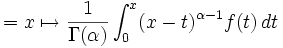Cálculo fraccional

Cálculo fraccional

Cálculo fraccional

En matemáticas, el cálculo fraccional es una rama del análisis matemático que estudia la posibilidad de tomar potencias reales del operador diferencial

D = \frac{d}{dx} ,

y el operador integral J. (Usualmente no I, para evitar confusión con otros I-como glifos, o identidades; pero J no debe ser confundida con las funciones de Bessel, las que surgen frecuentemente en el estudio de las ecuaciones diferenciales.)

En este contexto potencias se refieren a la aplicación iterativa, en el mismo sentido que f2(x) = f(f(x)).
Por ejemplo, uno podría presentar la pregunta de interpretar con algún sentido

\sqrt{D} = D^{1/2} ,

como una raíz cuadrada del operador diferencial (un operador medio iterado), es decir, una expresión para algún operador que al ser aplicada dos veces a una función tendrá el mismo efecto que la diferenciación. Más generalmente, uno puede mirar la cuestión de definir

D^s \,

para valores reales de s de manera tal que cuando s toma como valor un número natural n, la potencia usual de la n-diferenciación se recupera para n > 0, y la −n potencia de J cuando n < 0.

Hay varias razones para considerar esta pregunta. Una de ellas es que de esta forma el semigrupo de potencias Dn en la variable discreta n son vistas dentro de un semigrupo continuo (eso se espera) de parámetro s, el cual es un número real. Los semigrupos continuos prevalecen en matemáticas, y tienen una teoría interesante. Nótese aquí que fracción es entonces una mala denominación para el exponente, ya que no necesita ser un número racional, pero el término cálculo fraccional se ha vuelto tradicional.

Contenido

Derivada fraccional

Respecto de la existencia de tal teoría, los fundamentos de esta materia fueron sentados por Liouville en una obra de 1832. La derivada fraccional de una función al orden a es ahora frecuentemente definida por medio de las transformadas integrales de Fourier o la Mellin. Un punto importante es que la derivada fraccional en un punto x es una propiedad local solamente cuando a es un natural; en casos no integrales no podemos decir que la derivada fraccional en x de una función f depende solamente del gráfico de f muy cerca de x, de la forma en que las derivadas que son potencias de integrales ciertamente lo hacen. Entonces, se espera que la teoría incluya algún tipo de condiciones de frontera, incluyendo información sobre la función más lejos. Para usar una metáfora, la derivada fraccional requiere algo de visión periférica.

Acerca de la historia del tema, se puede consultar la tesis (en francés): Stéphane Dugowson, Les différentielles métaphysiques (histoire et philosophie de la généralisation de l'ordre de dérivation), Thèse, Université Paris Nord (1994)

Heurística

Una pregunta bastante natural sería, existe un operador H, o media derivada, tal que

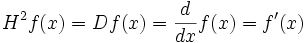H^2 f(x) = D f(x) = \frac{d}{dx} f(x) = f'(x) ?

Resulta que sí existe tal operador, y ciertamente para cualquier a > 0, existe un operador P tal que

(P ^ a f)(x) = f'(x) \,

o para expresarlo de otra manera, 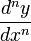\frac{d^ny}{dx^n} está bien definida para todos los valores reales de n > 0. Un resultado similar se aplica a la integración.

Para profundizar en cierto detalle, comiéncese con la Función gamma \Gamma \,, la cual se define tal que

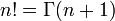n! = \Gamma(n+1) \,.

Asumiendo una función f(x) que está bien definida cuando x > 0, podemos formar la integral definida desde 0 hasta x. Llamémos a esto

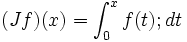( J f ) ( x ) = \int_0^x f(t) ; dt .

Repitiendo este proceso se tiene

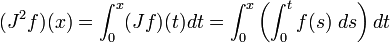( J^2 f ) ( x ) = \int_0^x ( J f ) ( t ) dt = \int_0^x \left( \int_0^t f(s) \; ds \right) dt,

y esto puede ser extendido arbitrariamente.

La fórmula de Cauchy para integración repetida, es decir

(J^n f) ( x ) = { 1 \over (n-1) ! } \int_0^x (x-t)^{n-1} f(t) ; dt,

conduce a una manera sencilla para la generalización a todo n.

Usando simplemente la función Gamma para eliminar la naturaleza discreta de la función factorial se obtiene un candidato natural para aplicaciones fraccionales del operador integral.

(J^\alpha f) ( x ) = { 1 \over \Gamma ( \alpha ) } \int_0^x (x-t)^{\alpha-1} f(t) \ dt

Este es de hecho un operador bien definido.

Puede ser demostrado que el operador J es conmutativo y aditivo. Esto es,

(J^\alpha) (J^\beta) f = (J^\beta) (J^\alpha) f = (J^{\alpha+\beta} ) f = { 1 \over \Gamma ( \alpha + \beta) } \int_0^x (x-t)^{\alpha+\beta-1} f(t) \; dt

Esta propiedad se denomina la propiedad de semigrupo de los operadores diferintegrales fraccionales. Lamentablemente el proceso comparable para el operador derivada D es considerablemente más complejo, pero puede ser demostrado que D no es ni conmutativo, ni aditivo en general.

Media derivada de una función simple

Asumamos que f(x) es un monomio de la forma

f(x) = x^k\;.

La primer derivada, como es usual, es

f'(x) = {d \over dx } f(x) = k x^{k-1}\;.

Repitiendo esto se obtiene el resultado general

{d^a \over dx^a } x^k = { k! \over (k - a) ! } x^{k-a}\;,

El cual, luego de reemplazar los factoriales con la función Gamma, nos lleva a

{d^a \over dx^a } x^k = { \Gamma(k+1) \over \Gamma(k - a + 1) } x^{k-a}\;.

Entonces, por ejemplo, la media derivada de x es

{ d^{1 \over 2} \over dx^{1 \over 2} } x = { \Gamma(1 + 1) \over \Gamma ( 1 - {1 \over 2} + 1 ) } x^{1-{1 \over 2}} = { \Gamma( 2 ) \over \Gamma ( { 3 \over 2 } ) } x^{1 \over 2} = {2 \pi^{-{1 \over 2}}} x^{1 \over 2}\;.

Repitiendo este proceso obtenemos

{ d^{1 \over 2} \over dx^{1 \over 2} } {2 \pi^{-{1 \over 2}}} x^{1 \over 2} = {2 \pi^{-{1 \over 2}}} { \Gamma ( 1 + {1 \over 2} ) \over \Gamma ( {1 \over 2} - { 1 \over 2 } + 1 ) } x^{{1 \over 2} - {1 \over 2}} = {2 \pi^{-{1 \over 2}}} { \Gamma( { 3 \over 2 } ) \over \Gamma ( 1 ) } x^0 = { 1 \over \Gamma (1) } = 1,

el cual es realmente el resultado esperado de

\left( \frac{d^{1/2}}{dx^{1/2}} \frac{d^{1/2}}{dx^{1/2}} \right) x = { d \over dx } x = 1 \,

Transformada de Laplace

También se puede llegar a la cuestión mediante la transformada de Laplace. Notando que

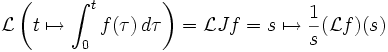\mathcal L\left(t\mapsto\int_0^t f(\tau)\,d\tau\right)=\mathcal LJf=s\mapsto\frac1s(\mathcal Lf)(s), y
\mathcal LJ^2f=s\mapsto\frac1s(\mathcal LJf)(s)=s\mapsto\frac1{s^2}(\mathcal Lf)(s)

etc., enunciamos que

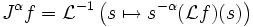J^\alpha f=\mathcal L^{-1}\left(s\mapsto s^{-\alpha}(\mathcal Lf)(s)\right).

Por ejemplo

J^\alpha\left(t\mapsto t^k\right) =\mathcal L^{-1}\left(s\mapsto{\Gamma(k+1)\over s^{\alpha+k+1}}\right) =t\mapsto{\Gamma(k+1)\over\Gamma(\alpha+k+1)}t^{\alpha+k}

como era de esperarse. De hecho, dada la regla de convolución

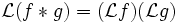\mathcal L(f*g)=(\mathcal Lf)(\mathcal Lg) (y abreviando p(x) = xα − 1 por claridad) encontramos que

J^\alpha f=\frac1{\Gamma(\alpha)}\mathcal L^{-1}\left(\left(\mathcal Lp\right)(\mathcal Lf)\right) =\frac1{\Gamma(\alpha)}(p*f) =x\mapsto\frac1{\Gamma(\alpha)}\int_0^xp(x-t)f(t)\,dt =x\mapsto\frac1{\Gamma(\alpha)}\int_0^x(x-t)^{\alpha-1}f(t)\,dt

que es lo que Cauchy nos ha dado anteriormente.

Las transformadas de Laplace "funcionan" en relativamente pocas funciones, pero son frecuentemente útiles al resolver ecuaciones diferenciales fraccionales.

Diferintegral de Riemann-Liouville

La forma clásica del cálculo fraccional nos es dada por la diferintegral de Riemann-Liouville, esencialmente lo que ha sido descrito arriba. La teoría para funciones periódicas, incluyendo por tanto la 'condición de frontera' de repetirse tras un período, es la diferintegral de Weyl. Se define sobre series de Fourier y requier el coeficiente constante de Fourier para desaparecer (entonces, se aplica a funciones en el círculo unidad integrando a 0).

Por contraste con la diferintegral de Grunwald-Letnikov comienza con la derivada.

Cálculo funcional

En el contexto del análisis funcional, las funciones f(D) más generales que potencias se estudian en el cálculo funcional de la teoría espectral. La teoría de operadores pseudo-diferenciales también le permite a uno considerar potencias de D. Los operadores resultantes son ejemplos de operadores singulares integrales; y la generalización de la teoría clásica a mayores dimensiones es llamada la teoría de los potenciales de Riesz. Entonces hay una cantidad de teorías contemporáneas disponibles, dentro de las cuales el cálculo fraccional puede discutirse. Vea también el operador de Erdelyi-Kober, importante en la teoría de las funciones especiales.

Para posibles interpretaciones geométricas y físicas de la integración y diferenciación de orden fraccional, vea:

Referencias

  • Theory and Applications of Fractional Differential Equations, by Kilbas, A. A.; Srivastava, H. M.; and Trujillo, J. J. Amsterdam, Netherlands, Elsevier, Febrary 2006. ISBN 0-444-51832-0 (http://www.elsevier.com/wps/find/bookdescription.cws_home/707212/description#description)
  • An Introduction to the Fractional Calculus and Fractional Differential Equations, por Kenneth S. Miller, Bertram Ross (Editor). Tapa dura: 384 pages. Editorial: John Wiley & Sons; 1ª edición (May 19, 1993). ISBN 0-471-58884-9
  • The Fractional Calculus; Theory and Applications of Differentiation and Integration to Arbitrary Order (Mathematics in Science and Engineering, V), por Keith B. Oldham, Jerome Spanier. Tapa dura. Editorial: Academic Press; (November 1974). ISBN 0-12-525550-0
  • Fractional Differential Equations. An Introduction to Fractional Derivatives, Fractional Differential Equations, Some Methods of Their Solution and Some of Their Applications., (Mathematics in Science and Engineering, vol. 198), por Igor Podlubny. Tapa dura. Editorial: Academic Press; (October 1998) ISBN 0-12-558840-2
  • Fractals and Fractional Calculus in Continuum Mechanics, by A. Carpinteri (Editor), F. Mainardi (Editor). Paperback: 348 pages. Publisher: Springer-Verlag Telos; (January 1998). ISBN 3-211-82913-X
  • Physics of Fractal Operators, por Bruce J. West, Mauro Bologna, Paolo Grigolini. Tapa dura: 368 pages. Editorial: Springer Verlag; (January 14, 2003). ISBN 0-387-95554-2
  • Fractional Calculus and the Taylor-Riemann Series, Rose-Hulman Undergrad. J. Math. Vol.6(1) (2005).
  • Operator of fractional derivative in the complex plane, by Petr Zavada, Commun.Math.Phys.192, pp. 261-285,1998. doi:10.1007/s002200050299 (available online or as the arXiv preprint)
  • Relativistic wave equations with fractional derivatives and pseudodifferential operators, by Petr Zavada, Journal of Applied Mathematics, vol. 2, no. 4, pp. 163-197, 2002. doi:10.1155/S1110757X02110102 (available online or as the arXiv preprint)

Véase también

  • Diferintegral
  • Ecuaciones diferenciales fraccionales

Enlaces externos

Obtenido de "C%C3%A1lculo fraccional"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Cálculo — Saltar a navegación, búsqueda Para otros usos de este término, véase Cálculo (desambiguación). Para cálculo infinitesimal (diferencial o integral) véase Cálculo infinitesimal Para el estudio de los números reales, los complejos, los vectores y… …   Wikipedia Español

  • Cálculo (desambiguación) — Saltar a navegación, búsqueda Cálculo puede referirse a: En Matemática: Cálculo infinitesimal es la rama base del análisis matemático. Se divide a su vez en: Cálculo diferencial Cálculo integral Cálculo, algoritmo mediante el cual se conocen las… …   Wikipedia Español

  • Polinomios de Legendre — Saltar a navegación, búsqueda En matemáticas al resolver la formula de Rodrigues, las Funciones de Legendre son las soluciones a las Ecuaciones Diferenciales de Legendre: llamadas así por el matemático francés Adrien Marie Legendre. Estas… …   Wikipedia Español

  • Función gamma — en el eje real. Valor absoluto de la función gamma en el plano complejo …   Wikipedia Español

  • Media iteración — La media iterada de una función f (denotada por f1/2) es cualquier función que satisfaga lo siguiente f1/2(f1/2(x)) = f(x) La media iteración es un caso especial de iteración fraccional de funciones. Para un ejemplo de este uso, vea el artículo… …   Wikipedia Español

  • Edad del Universo — Saltar a navegación, búsqueda La edad del Universo, de acuerdo con la Teoría del Big Bang, es el tiempo transcurrido desde el Big Bang hasta el presente. El consenso de los científicos contemporáneos es sobre 13.600.000.000 años (trece mil… …   Wikipedia Español

  • Teoría austríaca del ciclo económico — La teoría austríaca del ciclo económico (TACE) fue desarrollada por economistas de la escuela de Viena, incluidos F.A. Hayek y L.V. Mises. Explica la relación entre el crédito bancario, el crecimiento económico y los errores de inversión masivos… …   Wikipedia Español

  • Derivada — La derivada de la función en el punto marcado equivale a la pendiente de la recta tangente (la gráfica de la función está dibujada en negro; la tangente a la curva está dibujada en rojo). En matemáticas, la derivada de una función es una medida… …   Wikipedia Español

  • Fórmula de Bailey-Borwein-Plouffe — La fórmula de Bailey Borwein Plouffe (o fórmula BBP) permite calcular el enésimo dígito de π en base 2 (o 16) sin necesidad de hallar los precedentes, de una manera rápida y utilizando muy poco espacio de memoria en la computadora. Simon Plouffe… …   Wikipedia Español

  • C.H. Douglas — C.H. Douglas. Clifford Hugh Douglas (20 de enero de 1879 29 de septiembre de 1952) fue un oficial (mayor) en el ejército británico, ingeniero mecánico e industrial, y pionero del movimiento por el crédito social y la democracia económica …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”