- Descomposición (matemática)
-
Descomposición (matemática)
En la matemática, descomponer objetos es una generalización del proceso de factorización y dependiendo del área especifica, se adjetiviza:
Con números, e.g. 6=2x3 indica que 6 se puede decomponer (factorizar) con 2 y 3 mediante la multiplicación ordinaria. Cada número natural tiene una única descomposición en factores primos, esto es el enunciado del teorema fundamental de la aritmética. En el álgebra elemental: a2 − b2 = (a + b)(a − b), recibe en nombre producto notable, que es otro tipo de descomposición en factores de orden menor.
Dado un conjunto y una relación de equivalencia en él, el conjunto cociente en una descomposición por partición del conjunto es sus diferentes clases de equivalencia (Lema de abstracción). En álgebra lineal uno habla de las descomposición de valor singular, la descomposiciones en eigen-espacios o las descomposiciones canónicas de Jordan. En un grupo, la relación de conjugación
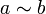si y sólo si a = gbg − 1 descompone al grupo en clases de conjugación llamadas también órbitas.
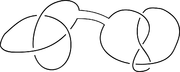
Suma conexa 2-dimensional
En topología se tiene la descomposición de variedades mediante el proceso de Heegaard. En la topología de dimensiones bajas las descomposiciones de Heegaard es una técnica para entender las propiedades topológicas de las variedades en general. Como ejemplo: para 3-variedades orientables, un tipo de descomposición, consiste en encontrar el par de cubos con asas -homeomorfos, que decomponen a la variedad M de la forma;
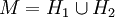, con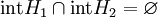 
. Esto equivale pedir que ambas fronteras 
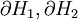sean superficies del mismo género.Otro tipo descomposición para una tres variedad es mediante sumas conexas de variedades primas. La imagen de al lado ilustra el proceso en dimensión dos.
Véase también:
Suma conexa de nudos- asa (matemática)
- tri-género
- descomposición
Categoría: Topología geométrica
Wikimedia foundation. 2010.
