Distribución binomial negativa

Distribución binomial negativa: Distribución binomial negativa

Saltar a navegación, búsqueda

Binomial negativa
Función de probabilidad

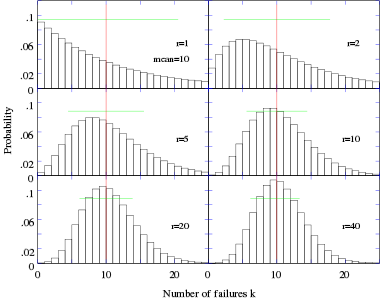
La línea roja representa la media, y la verde tiene una longitud de aproximadamente 2σ.

Función de distribución de probabilidad

Parámetros 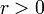$r > 0\!$ (real)
$0<p<1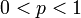\!$ (real)

Dominio 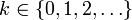$k \in \{0,1,2,\ldots\}\!$

Función de probabilidad (fp) 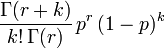$\frac{\Gamma(r+k)}{k!\,\Gamma(r)}\,p^r\,(1-p)^k \!$

Función de distribución (cdf) $I p (r, k + 1) donde I p (x, y)$ es la función beta incompleta regularizada

Media 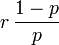$r\,\frac{1-p}{p}$

Mediana

Moda 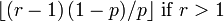$\lfloor(r-1)\,(1-p)/p\rfloor\text{ if }r>1$
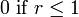
$0\text{ if }r\leq 1$

Varianza 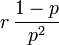$r\,\frac{1-p}{p^2}$

Coeficiente de simetría 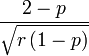$\frac{2-p}{\sqrt{r\,(1-p)}}\!$

Curtosis 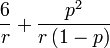$\frac{6}{r} + \frac{p^2}{r\,(1-p)}\!$

Entropía

Función generadora de momentos (mgf) 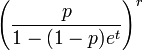$\left(\frac{p}{1-(1-p) e^t}\right)^r \!$

Función característica 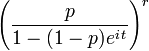$\left(\frac{p}{1-(1-p) e^{i\,t}}\right)^r \!$

En estadística la distribución binomial negativa es una distribución de probabilidad discreta que incluye a la distribución de Pascal.

El número de experimentos de Bernoulli de parámetro $θ$ independientes realizados hasta la consecución del k-ésimo éxito es una variable aleatoria que tiene una distribución binomial negativa con parámetros k y $θ$ .

La distribución geométrica es el caso concreto de la binomial negativa cuando k = 1.

Propiedades

Su función de probabilidad es

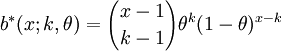
$\! \ b^*(x;k,\theta) = {x-1 \choose k-1}\theta^k(1-\theta)^{x-k}$

para enteros x mayores o iguales que k, donde

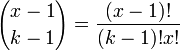$\!{x-1 \choose k-1} = \frac{(x-1)!}{(k-1)!x!}$ .

Su media es

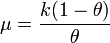
$\!\mu = \frac{{k(1 - \theta )}}{\theta}$

si se piensa en el número de fracasos únicamente y

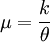
$\!\mu = \frac{{k}}{\theta}$

si se cuentan también los k-1 éxitos.

Su varianza es

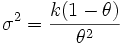
$\!\sigma ^2 = \frac{{k(1 - \theta )}}{{\theta ^2 }}$

en ambos casos.

Ejemplos

Si la probabilidad de que un niño expuesto a una enfermedad contagiosa la contraiga es 0,40, ¿cuál es la probabilidad de que el décimo niño expuesto a la enfermedad sea el tercero en contraerla? En este caso, X es el número de niños expuestos la enfermedad y

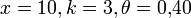
$\!x = 10, k = 3, \theta = 0,\!40$

La solución es:

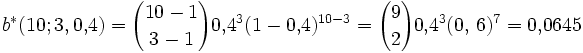$\!b^*(10;3,0,\!4)={10-1 \choose 3-1}0,\!4^3(1-0,\!4)^{10-3}={9 \choose 2}0,\!4^3(0,\,6)^{7}=0,\!0645$

Obtenido de "Distribuci%C3%B3n binomial negativa"

Categoría: Distribuciones discretas

Binomial negativa
Función de probabilidad La línea roja representa la media, y la verde tiene una longitud de aproximadamente 2σ.
Función de distribución de probabilidad
Parámetros	$r > 0\!$ (real) $0<p<1\!$ (real)
Dominio	$k \in \{0,1,2,\ldots\}\!$
Función de probabilidad (fp)	$\frac{\Gamma(r+k)}{k!\,\Gamma(r)}\,p^r\,(1-p)^k \!$
Función de distribución (cdf)	$I p (r, k + 1) donde I p (x, y)$ es la función beta incompleta regularizada
Media	$r\,\frac{1-p}{p}$
Mediana
Moda	$\lfloor(r-1)\,(1-p)/p\rfloor\text{ if }r>1$ $0\text{ if }r\leq 1$
Varianza	$r\,\frac{1-p}{p^2}$
Coeficiente de simetría	$\frac{2-p}{\sqrt{r\,(1-p)}}\!$
Curtosis	$\frac{6}{r} + \frac{p^2}{r\,(1-p)}\!$
Entropía
Función generadora de momentos (mgf)	$\left(\frac{p}{1-(1-p) e^t}\right)^r \!$
Función característica	$\left(\frac{p}{1-(1-p) e^{i\,t}}\right)^r \!$

Игры ⚽ Нужно решить контрольную?

Mira otros diccionarios:

Distribución Binomial Negativa — En estadística, la distribución binomial negativa es una distribución de probabilidad discreta. El número de ensayos en que ocurre el késimo éxito es una variable aleatoria que tiene una distribución binomial negativa con parámetros k y . Donde k … Enciclopedia Universal
Distribución geométrica — Saltar a navegación, búsqueda En teoría de probabilidad y estadística, la distribución geométrica es cualquiera de las dos distribuciones de probabilidad discretas siguientes: la distribución de probabilidad del número X del ensayo de Bernoulli… … Wikipedia Español
Distribución logarítmica — Saltar a navegación, búsqueda En teoría de la probabilidad, la distribución logarítmica es una distribución de probabilidad discreta derivada de la expansión en series de Maclaurin A partir de ella, se obtiene Por lo tanto, los valores … Wikipedia Español
Distribución de probabilidad — La distribución Normal suele conocerse como la campana de Gauss . En teoría de la probabilidad y estadística, la distribución de probabilidad de una variable aleatoria es una función que asigna a cada suceso definido sobre la variable aleatoria… … Wikipedia Español
Distribución normal — Saltar a navegación, búsqueda Distribución normal Función de densidad de probabilidad La línea verde corresponde a la distribución normal estandar Función de distribución de probabilidad … Wikipedia Español
Familia exponencial — Saltar a navegación, búsqueda En probabilidad y estadística, la familia exponencial es una clase de distribuciones de probabilidad cuya formulación matemática puede expresarse de la manera que se especifica debajo. Esta formulación confiere a las … Wikipedia Español
Check Wikipedia — Wikiproyecto:Check Wikipedia Saltar a navegación, búsqueda Esta página contiene de forma consciente fallos ortográficos. Los bots no deben intentar corregirlos. Atajo PR:CWPR:CW … Wikipedia Español
Parámetro estadístico — Saltar a navegación, búsqueda La media aritmética … Wikipedia Español
Unidad Erlang — El Erlang es una unidad adimensional utilizada en telefonía como una medida estadística del volumen de tráfico. Recibe el nombre del ingeniero danés A. K. Erlang, pionero de la teoría de colas. El tráfico de un Erlang corresponde a un recurso… … Wikipedia Español
Molothrus ater — Tordo cabecicafé Macho adulto … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Distribución binomial negativa

Distribución binomial negativa

Propiedades

Ejemplos

Mira otros diccionarios:

Compartir el artículo y extractos

Los diccionarios y las enciclopedias sobre el Académico

Wikipedia Español

Distribución binomial negativa

Distribución binomial negativa

Propiedades

Ejemplos

Mira otros diccionarios:

Compartir el artículo y extractos

Link directo