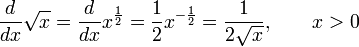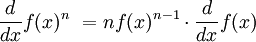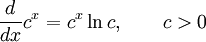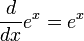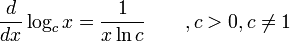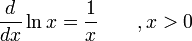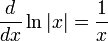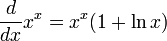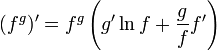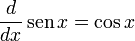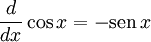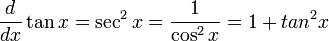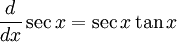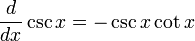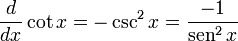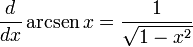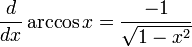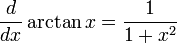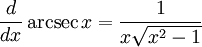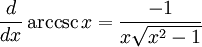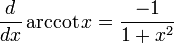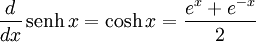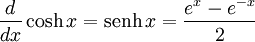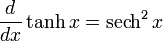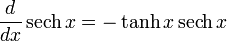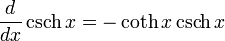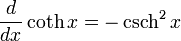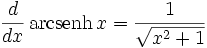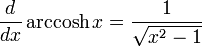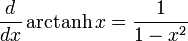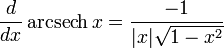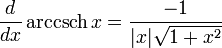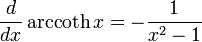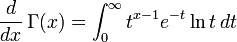- Derivadas
-
Anexo:Derivadas
La operación fundamental en el cálculo diferencial es encontrar una derivada. Esta tabla enlista las derivadas de varias funciones. En lo sucesivo, f y g son funciones de x y c es una constante con respecto a x. Se presupone al conjunto de los números reales. Estas fórmulas son suficientes para diferenciar cualquier función elemental.
Contenido
Reglas generales de diferenciación
Derivadas de funciones simples
- Derivada de la función inversa
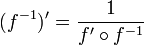 ,
,
para alguna función diferenciable f de un argumento real y con valores reales, cuando las composiciones indicadas e inversas existen.
Derivadas de funciones exponenciales y funciones logarítmicas
- Derivada de la función potencial exponencial
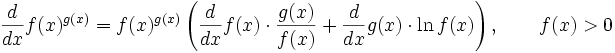
Derivadas de funciones trigonométricas
Para más detalles sobre este tema, véase Derivación de funciones trigonométricas.Derivadas de funciones hiperbólicas
a
Derivadas de funciones especiales
Función Gamma
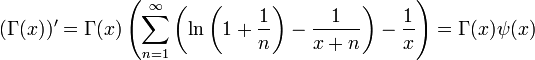
- Función Zeta de Riemann
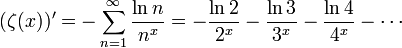
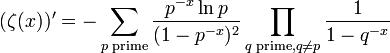 Categorías: Análisis matemático | Anexos:Matemáticas
Categorías: Análisis matemático | Anexos:Matemáticas
Wikimedia foundation. 2010.

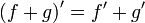
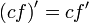
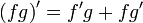
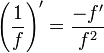
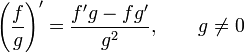
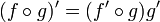
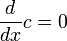
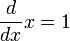
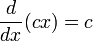
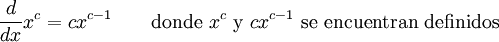
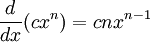
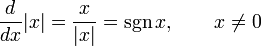
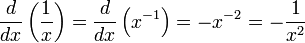
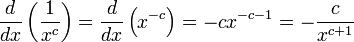
![{d \over dx}(\sqrt[n]{x}) = { 1 \over n \sqrt[n]{x^{n-1}} }\, \mbox{sea }x > 0](/pictures/eswiki/97/a02fbee278911cce8f7b017d1ee03fc9.png)