Transformación lineal de intervalos

Transformación lineal de intervalos
 Se ha sugerido que este artículo o sección sea fusionado en función lineal (discusión).
Una vez que hayas realizado la fusión de artículos, pide la fusión de historiales aquí.

La transformación lineal de intervalos es una aplicación lineal típica con usos variados como proyección de intervalos o planos. Por ejemplo, la transformación que lleva de un formato de video DVD con resolución de 720x570 pixeles a uno VCD con resolución de 352×240.

Contenido

Definición

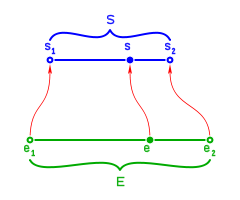
Transformación lineal del intervalo [e1,e2] al intervalo [s1,s2]

Sean:

E= [e_1,e_2] \; y
S= [s_1,s_2] \;

dos intervalos en \mathbb{R}. La transformación lineal:

T(x): [e_1,e_2] \rarr [s_1,s_2]; \; \forall x \in \mathbb{R}

esta dada por:

s_1 = m e_1 + b \; ---- eq(1)
s_2 = m e_2 + b \; ---- eq(2)

donde m y b son los parámetros de la transformación lineal

T(x)= mx+b ; \quad \forall x \in \mathbb{R} .

Resolviendo para eq(1) y eq(2):

b =s_1 - m e_1 ; b =s_2 - m e_2 \;
s_1 - m e_1 = s_2 - m e_2 \;
s_1 - s_2 = m( e_1 - e_2) \;
m=\frac{(s_1 - s_2)}{(e_1 - e_2)}
Función lineal de transformación

sustituyendo m\quad en eq(1):

s_1 = \frac{(s_1 - s_2)}{(e_1 - e_2)} e_1 + b \quad\Rightarrow b = s_1-\frac{(s_1 - s_2)}{(e_1 - e_2)} e_1

es decir:

T(x)= \frac{(s_1 - s_2)}{(e_1 - e_2)}x + \Bigg[ s_1-\frac{(s_1 - s_2)}{(e_1 - e_2)} e_1 \Bigg]

simplificando:

T(x)= \frac{(s_1 - s_2)}{(e_1 - e_2)}\; (x - e_1) + s_1

Ejemplo

Como ejemplo de esta transformación, supongamos que un programador de codecs desea transformar de un formato e video DVD a uno VCD, su problema consiste, entre otras cosas, en proyectar el intervalo horizontal [1,720] a otro intervalos horizontal [1,352]; para ello usa la transformación lineal Th(x) descrita arriba, de la siguiente manera:

e_1=1 \;
e_2=720 \;
s_1=1 \;
s_2=352\ ;

Sustituyendo en la expresión:

T(x)= \frac{(s_1 - s_2)}{(e_1 - e_2)}\; (x - e_1) + s_1

Obtendremos:

T_{h}(x)= \frac{(1 - 352)}{(1 - 720)}\; (x - 1) + 1

Simplificando las fracciones tendremos:

T_{h}(x)= \frac{351\; x + 368}{719}

Con lo que para cada x del intervalo [1,720] obtendremos un T(x) correspondiente del intervalo [1,352].

De igual manera para la transformación vertical Tv(x)

e_1 = 1 \;
e_2 = 570 \;
s_1 = 240 \;
s_2 = 1 \;

Partiendo de la relación:

T(x)= \frac{(s_1 - s_2)}{(e_1 - e_2)}\; (x - e_1) + s_1

y sustituyendo cada termino, tendremos:

T_{v}(x)= \frac{(240 - 1)}{(1 - 570)}\; (x - 1) + 240

Operando la expresión, tendremos:

T_{v}(x)= \frac{-239\; x + 136799}{569}

En este caso para x= 1, tendremos que T(x)= 240.

Véase también

Enlaces externos


Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Función lineal — Se ha sugerido que Transformación lineal de intervalos sea fusionado en este artículo o sección (discusión). Una vez que hayas realizado la fusión de artículos, pide la fusión de historiales aquí. Para la función entre dos espacios vectoriales… …   Wikipedia Español

  • Regresión no lineal — Saltar a navegación, búsqueda En estadística, la regresión no lineal es un problema de inferencia para un modelo tipo: basado en datos multidimensionales x,y, donde f es alguna función no lineal respecto a algunos parámetros desconocidos θ. Como… …   Wikipedia Español

  • Intervalo (matemática) — En matemáticas, un intervalo (del lat intervallum) es un conjunto comprendido entre dos valores. Específicamente, un intervalo real es un subconjunto conexo de la recta real, es decir, una porción de recta entre dos valores dados. Contenido 1… …   Wikipedia Español

  • Grupo diedral — Este copo de nieve tiene la simetría diedral de un hexágono regular. En matemáticas, un grupo diedral es el grupo de simetría de un polígono regular, incluyendo tanto rotaciones y reflexiones.[1] …   Wikipedia Español

  • Cálculo diferencial — Saltar a navegación, búsqueda El cálculo diferencial, un campo de las matemáticas, es el estudio de cómo cambian las funciones cuando sus variables cambian. El principal objeto de estudio en el cálculo diferencial es la derivada. Una noción… …   Wikipedia Español

  • Función convexa — en un intervalo [x,y]. En matemática, una función real f definida en un intervalo (o en cualquier subconjunto convexo de algún espacio vectorial) se llama función convexa o cóncava hacia arriba, si para dos puntos cualquiera x e y es su dominio C …   Wikipedia Español

  • Distribución normal — Saltar a navegación, búsqueda Distribución normal Función de densidad de probabilidad La línea verde corresponde a la distribución normal estandar Función de distribución de probabilidad …   Wikipedia Español

  • Historia del arte — Para la historiografía de la historia del arte, véase Estudio de la historia del arte. La creación …   Wikipedia Español

  • Orden (ejército) — Batalla de Handschuhsheim (24 de septiembre de 1795). Pintura de Friedrich Rottman. La palabra orden tiene varias acepciones en el ámbito militar. Contenido 1 …   Wikipedia Español

  • Corrimiento al rojo — Saltar a navegación, búsqueda Corrimiento al rojo de las líneas espectrales en el espectro visible de un supercúmulo de galaxias distantes (derecha), comparado con el del Sol (izquierda). La longitud de onda se incrementa hacia el rojo y más allá …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”