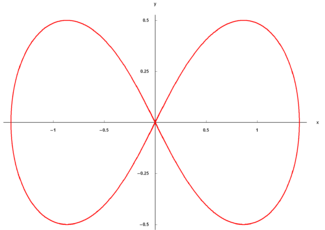
Lemniscata

En matemática, una lemniscata es un tipo de curva descrita por la siguiente ecuación en coordenadas cartesianas:

$(x^2 + y^2)^2 = 2a^2 (x^2 - y^2) \,$

La representación gráfica de esta ecuación genera una curva similar a $\infty$ . La curva se ha convertido en el símbolo del infinito y es ampliamente utilizada en matemática. El símbolo en sí mismo es, a veces, llamado lemniscata. Su representación en Unicode es ∞ y su código es (∞).

La lemniscata fue descrita por primera vez en 1694 por Jakob Bernoulli como la modificación de una elipse, curva que se define como el lugar geométrico de los puntos tales que la suma de las distancias desde dos puntos focales es una constante. En contraposición, una lemniscata es el lugar geométrico de los puntos tales que el producto de estas distancias es constante. Bernoulli la llamó lemniscus, que en Latín significa "cinta colgante".

La lemniscata puede ser obtenida como la transformada inversa de una hipérbola, con el círculo inversor centrado en el centro de la hipérbola (punto medio del segmento que une los dos focos).

Contenido

1 Otras ecuaciones
2 Derivadas
- 2.1 Con y como función de x
- 2.2 Con x como función de y
3 Parámetro arco y funciones elípticas
4 Véase también

Otras ecuaciones

La lemniscata puede ser descrita mediante coordenadas polares según la siguiente ecuación:

$r^2 = 2a^2 \cos 2\theta\,$

Análogamente, con coordenadas bipolares su ecuación es:

$rr' = \frac{a^2}{2}$

Derivadas

Cada derivada fué calculada usando Diferenciación implícita.

Con $y$ como función de $x$

$\frac{dy}{dx} = \begin{cases} \mbox{ilimitado} & \mbox{si } y = 0 \mbox{ y } x \ne 0 \\ \pm1 & \mbox{si } y = 0 \mbox{ y } x = 0 \\ \frac{x(a^2 - x^2 - y^2)}{y(a^2 + x^2 + y^2)} & \mbox{if } y \ne 0 \end{cases}$

$\frac{d^2y}{dx^2} = \begin{cases} \mbox{ilimitado} & \mbox{si } y = 0 \mbox{ y } x \ne 0 \\ 0 & \mbox{si } y = 0 \mbox{ y } x = 0 \\ \frac{3a^6(y^2 - x^2)}{y^3(a^2 + 2x^2 + 2y^2)^3} & \mbox{si } y \ne 0 \end{cases}$

Con $x$ como función de $y$

$\frac{dx}{dy} = \begin{cases} \mbox{ilimitado} & \mbox{si } 2x^2 + 2y^2 = a^2 \\ \pm1 & \mbox{si } x = 0 \mbox{ y } y = 0 \\ \frac{y(a^2 + 2x^2 + 2y^2)}{x(a^2 - 2x^2 - 2y^2)} & \mbox{más } \end{cases}$

$\frac{d^2x}{dy^2} = \begin{cases} \mbox{ilimitado} & \mbox{si } 2x^2 + 2y^2 = a^2 \\ 0 & \mbox{si } x = 0 \mbox{ y } y = 0 \\ \frac{3a^6(x^2 - y^2)}{x^3(a^2 - 2x^2 - 2y^2)^3} & \mbox{más } \end{cases}$

Parámetro arco y funciones elípticas

La determinación del parámetro arco de la lemniscata llevó a las integrales elípticas, que fueron descubiertas durante el siglo XVIII. Alrededor de 1800, las funciones elípticas que intervienen en estas integrales fueron estudiadas por Carl Friedrich Gauss. No serían publicadas hasta mucho tiempo después, pero se hacían alusiones a ellas en las notas de su obra Disquisitiones Arithmeticae. La base del retículo definido por los pares fundamentales de períodos (pares ordenados de números complejos) tiene una forma muy especial, siendo proporcional a los enteros de Gauss. Por esta razón el conjunto de funciones elípticas con el producto complejo por la unidad imaginaria se denomina conjunto lemniscático.

Véase también

Óvalo de Cassini

Categoría:

Curvas algebraicas

Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

lemniscată — lemniscátă s. f., pl. lemniscáte Trimis de siveco, 10.08.2004. Sursa: Dicţionar ortografic LEMNISCÁTĂ s.f. (mat.) Curbă loc geometric al punctelor pentru care produsul distanţelor lor la două puncte fixe este constant. [< fr. lemniscate, cf … Dicționar Român
lemniscata — (Del lat. lemniscāta, adornada con la cinta llamada lemnisco). f. Curva plana de forma semejante a un 8 … Diccionario de la lengua española
Lemniscata — Lem nis*ca ta (l[e^]m n[i^]s*k[=a] t[.a]), Lemniscate Lem*nis cate (l[e^]m*n[i^]s k[asl]t), n. [L. lemniscatus adorned with ribbons, fr. lemniscus a ribbon hanging down, Gr. lhmni skos.] (Geom.) A curve in the form of the figure 8, with both… … The Collaborative International Dictionary of English
lemniscata — s. f. Curva geométrica em forma de 8 … Dicionário da Língua Portuguesa
Lemniscata — ► sustantivo femenino GEOMETRÍA Curva plana que tiene una forma semejante a un ocho. * * * lemniscata (del lat. «lemniscāta», adornada con lemnisco) f. Geom. *Curva plana de figura de ocho. ⊚ Se emplea para designar o describir esa *forma. * * *… … Enciclopedia Universal
lemniscata — n. [Gr. lemniskos, ribbon] A clubshaped organ … Dictionary of invertebrate zoology
lemniscata — lem·ni·scà·ta s.f. TS mat. curva piana a forma di otto {{line}} {{/line}} DATA: 1834. ETIMO: der. di lemniscato … Dizionario italiano
lemniscata — pl.f. lemniscate … Dizionario dei sinonimi e contrari
Durvilledoris lemniscata — Scientific classification Kingdom: Animalia Phylum: Mollusca Class: Gastropoda … Wikipedia
Lemniscate — Lemniscata Lem nis*ca ta (l[e^]m n[i^]s*k[=a] t[.a]), Lemniscate Lem*nis cate (l[e^]m*n[i^]s k[asl]t), n. [L. lemniscatus adorned with ribbons, fr. lemniscus a ribbon hanging down, Gr. lhmni skos.] (Geom.) A curve in the form of the figure 8,… … The Collaborative International Dictionary of English

Los diccionarios y las enciclopedias sobre el Académico

Lemniscata