- Distribución hipergeométrica
-
Distribución hipergeométrica
Distribución hipergeométrica Función de distribución de probabilidad Parámetros 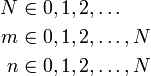
Dominio 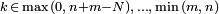
Función de probabilidad (fp) 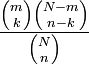
Función de distribución (cdf) Media 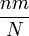
Mediana Moda 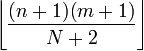
Varianza 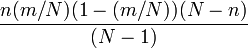
Coeficiente de simetría ![\frac{(N-2m)(N-1)^\frac{1}{2}(N-2n)}{[nm(N-m)(N-n)]^\frac{1}{2}(N-2)}](/pictures/eswiki/99/cbc5d8105638f44a15bb6b6a42c98834.png)
Curtosis ![\left[\frac{N^2(N-1)}{n(N-2)(N-3)(N-n)}\right]](/pictures/eswiki/98/b5c85bfac379f6390cf9ac846b3643cc.png)
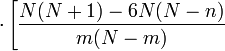
![+\left.\frac{3n(N-n)(N+6)}{N^2}-6\right]](/pictures/eswiki/53/5eea883c0354dcf5301ca80d816a58c2.png)
Entropía Función generadora de momentos (mgf) 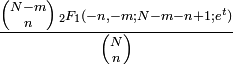
Función característica 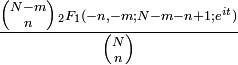
En teoría de la probabilidad la distribución hipergeométrica es una distribución discreta relacionada con muestreos aleatorios y sin reemplazo. Supóngase que se tiene una población de N elementos de los cuales, d pertenecen a la categoría A y N-d a la B. La distribución hipergeométrica mide la probabilidad de obtener x (
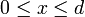 ) elementos de la categoría A en una muestra de n elementos de la población original.
) elementos de la categoría A en una muestra de n elementos de la población original.Propiedades
La función de probabilidad de una variable aleatoria con distribución hipergeométrica puede deducirse a través de razonamientos combinatorios y es igual a
donde N es el tamaño de población, n es el tamaño de la muestra extraída, d es el número de elementos en la población original que pertenecen a la categoría deseada y x es el número de elementos en la muestra que pertenecen a dicha categoría. La notación
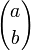 hace referencia al coeficiente binomial, es decir, el número de combinaciones posibles al seleccionar b elementos de un total a.
hace referencia al coeficiente binomial, es decir, el número de combinaciones posibles al seleccionar b elementos de un total a.El valor esperado de una variable aleatoria X que sigue la distribución hipergeométrica es
y su varianza,
En la fórmula anterior, definiendo
y
se obtiene
La distribución hipergeométrica es aplicable a muestreos sin reemplazo y la binomial a muestreos con reemplazo. En situaciones en las que el número esperado de repeticiones en el muestreo es presumiblemente bajo, puede aproximarse la primera por la segunda. Esto es así cuando N es grande y el tamaño relativo de la muestra extraída, n/N, es pequeño.
Categoría: Distribuciones discretas
Wikimedia foundation. 2010.

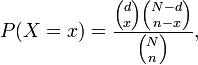
![E[X]=\frac{nd}{N}](/pictures/eswiki/101/edb7931c237719680795389c71e2ca37.png)
![Var[X]=\bigg(\frac{N-n}{N-1}\bigg)\bigg(\frac{nd}{N}\bigg)\bigg( 1-\frac{d}{N}\bigg).](/pictures/eswiki/57/9b21150dd51ee2e8e3c219b9d6c67cdd.png)
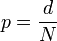
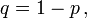
![Var[X]=npq\frac{N-n}{N-1}.](/pictures/eswiki/56/8450776365971ac3ed36f95d91b68b22.png)