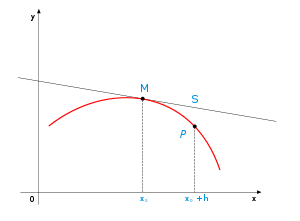
Función cóncava

Función cóncava
Adjacent concave function.svg

En matemática, una función es cóncava cuando dados dos puntos cualesquiera, el segmento que los une queda por debajo de la curva. Presenta su concavidad hacia abajo.[1] Una función cóncava es lo opuesto de una función convexa.

Contenido

Definición

Formalmente, una función real f definida en un intervalo (o en cualquier conjunto convexo C de algún espacio vectorial) se dice que es cóncava, si para dos puntos x e y cualesquiera definidas en su dominio C, y para cualquier t en [0,1], se cumple

f(tx+(1-t)y)\geq t f(x)+(1-t)f(y).

Además, f(x) es cóncavo en [a, b] si y sólo si la función −f(x) es convexa en [a, b].

Una función que es cóncava es a menudo también llamada cóncava hacia abajo, mientras que una función convexa es llamada cóncava hacia arriba.

Una función es estrictamente cóncava si

f(tx + (1-t)y) > t f(x) + (1-t)f(y)\,

para cualquier t en (0,1) y x ≠ y.

Una función continua en C es cóncava si y sólo si

f\left( \frac{x+y}2 \right) \ge \frac{f(x) + f(y)}2 .

para cualquier x e y en C.

Una función diferenciable f es cóncava en un intervalo si su derivada f ′ es monótonamente decreciente en ese intervalo: una función cóncava posee una pendiente negativa o decreciente. (entendiendo por "decreciente" aquí a que es "no-creciente", en lugar de "estrictamente decreciente"; es decir, se permite la pendiente cero).

Propiedades

Dada una función f doblemente diferenciable, si su segunda derivada f ′′(x) es positiva, entonces f es convexa; si f ′′(x) es negativa, entonces es cóncava. Los puntos donde la concavidad cambia son puntos de inflexión.

Si una función convexa (es decir, cóncava hacia arriba) tiene un "fondo" ("bottom"), cualquier punto al fondo es un mínimo extremo. Si una función cóncava (es decir, cóncava hacia abajo) tiene un "ápice" ("apex"), cualquier punto al ápice es un máximo extremo.

Si f(x) es doblemente diferenciable, entonces f(x) es cóncavo si y sólo si f ′′(x) es negativo o cero. Si su segunda derivada es negativa entonces es estrictamente cóncava, pero lo opuesto no es cierto, como podemos ver para f(x) = -x4.

Una función es cuasi-cóncava si y sólo si posee un x0 tal que para todo x < x0, f(x) es no-decreciente y para todo x > x0 es no-creciente. x0 puede también ser \pm \infty, haciendo la función no-decreciente (no-creciente) para todo x. Además, una función f es cuasi-convexa si y sólo si −f es cuasi-cóncava.

Ejemplos

  • La función f(x) = − x2 es cóncava, pues su segunda derivada es siempre negativa.
  • Cualquier función constante f(x) = c es cóncava y convexa.
  • La función f(x) = sin x es cóncava en cualquier intervalo de la forma [2\pi n, 2\pi n+\pi],\, donde n es un entero.

Véase también

Referencias

  1. ↑ Concavidad en descartes.cnice.mec.es

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Función convexa — en un intervalo [x,y]. En matemática, una función real f definida en un intervalo (o en cualquier subconjunto convexo de algún espacio vectorial) se llama función convexa o cóncava hacia arriba, si para dos puntos cualquiera x e y es su dominio C …   Wikipedia Español

  • Función real — Una función real es una función matemática cuyo dominio y codominio están contenidos en , es decir, es una función: En general se trata de funciones continuas, o bien discontinuas cuando están representadas por tramos, a diferencia de las… …   Wikipedia Español

  • Función matemática — En la imagen se muestra una función entre un conjunto de polígonos y un conjunto de números. A cada polígono le corresponde su número de lados. En matemáticas, se dice que una magnitud o cantidad es función de otra si el valor de la primera… …   Wikipedia Español

  • Gráfica de una función — En matemáticas, la gráfica de una función: es la visualización de la correspondencia entre los elementos del conjunto dominio y los del conjunto imagen mediante su representación iconográfica. También puede definirse como el conjunto formado por… …   Wikipedia Español

  • Concavidad — En geometría, la concavidad de una curva o de una superficie es la parte que se asemeja a la zona interior de una circunferencia o de una esfera.[1] Es el concepto complementario al de convexidad. Contenido 1 Ángulos cóncavos …   Wikipedia Español

  • Matriz hessiana — En Matemática, la matriz hessiana de una función f de n variables, es la matriz cuadrada de n × n, de las segundas derivadas parciales. Contenido 1 Definición 2 Aplicación de la matriz hessiana 2.1 Concavidad/Convexidad …   Wikipedia Español

  • Capacidad de canal — Saltar a navegación, búsqueda En Teoría de la Información, la capacidad de un canal de comunicación es la cantidad máxima de información que puede transportar dicho canal de forma fiable, es decir, con una probabilidad de error tan pequeña como… …   Wikipedia Español

  • Logaritmo — Logaritmos Gráfica de Logaritmos Definición …   Wikipedia Español

  • Cuchara — (Del lat. cochlear, aris < cochlea, concha, por la forma de la cuchara.) ► sustantivo femenino 1 Utensilio para comer, que consiste en un mango con una palita cóncava en un extremo: ■ trae la cuchara para tomar la sopa. TAMBIÉN cuchar 2… …   Enciclopedia Universal

  • Criterio de la segunda derivada — Saltar a navegación, búsqueda El Criterio o prueba de la segunda derivada es un teorema o método del cálculo matemático en el que se utiliza la segunda derivada para efectuar una prueba simple correspondiente a los máximos y mínimos relativos. Se …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”